本系列笔记仅为个人备忘记录，若要获得最大学习效果仍建议学习郑益慧老师课程：
郑益慧老师课程
如有谬误、补充，还望不吝指正

前面说到，集成运放是一个非常非常大放大倍数的放大电路，它非常容易饱和，如果开环的情况下只要一点点电压就可以让它饱和，为了能够使用它我们需要让它工作在线性区，为了让它工作在线性区，我们就需要反馈放大电路

1 基本概念及判断

1.1 基本概念

1.1.1 反馈

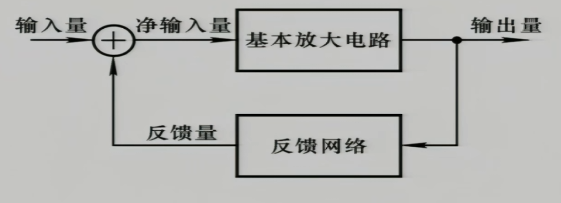
系统的输出量的一部分或全部被引回到输入端去影响输入，它只与输出有关，反馈量是输出的函数，反馈系统是个闭环系统

1.1.2 正、负反馈

1.1.2.1 正反馈

输出转一圈回来以反馈量的形式增加了净输入量增量，把增量推波助澜

1.1.2.2 负反馈

输出转一圈回来以反馈量的形式减少了净输入量增量，把增量往下拉

1.1.3 交直流反馈

1.1.3.1 直流反馈

直流通路里存在的反馈就是直流反馈，比如加旁路电容的 Q 点稳定的放大电路，$r_{e}$就只在直流里发挥反馈作用

1.1.3.2 交流反馈

交流通路里存在的反馈就是交流反馈

1.2 判断

1.2.1 反馈的存在与否

• 形式结构上：我要把输出的东西拉回到输入，那么输出到输入应该有一个通路来完成这种连接
• 关系上：存在一个反馈量在输入端影响输入，并且这个反馈量还只与输出相关，是输出量的函数

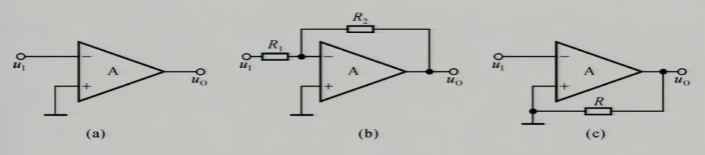
比如这三个图：

• (a)：从结构上，没有这么一条通路连接输出和输入，输出量和输入量就没有关系，显然不存在反馈
• (b)：结构上确实有一条通路从输入连到了输入，并且如果我们用叠加定理去看，把$u_{o}$看做一个电压源，置零$u_{1}$，则运放的输入端确实出现了一个只由$u_{o}$影响的信号$\frac{R_{1}}{R_{1}+R_{2}}u_{o}$，所以这个电路存在反馈
• (c)：结构上有通路存在，但是其实运放下面的输入口的电位一直是地，应该没有一个$u_{o}$影响的信号输入，所以这个电路没有反馈

1.2.2 反馈的极性

1.2.2.1 净输入量输入端

对于一个集成运放来说，输入端是两个输入端子，净输入量有两个一个$u_{P}$，一个$u_{N}$

对于一个三极管来说，输入端是基极和射级，净输入量是$u_{BE}$

对于一个差放来说，输入端是两边管子的基极

1.2.2.2 瞬时极性法

瞬时极性法，假如本来我们要分析$\Delta$的增长即一个正的增量，如果我们把直流拿掉，那么这个$\Delta$的增长实际上就是交流的一个瞬时的正极性 (正半轴)，然后从输入开始标记此时的瞬时极性直到输入 (对于运放，三极管，差分等的瞬时极性分析见原视频)

1.2.2.3 判别流程 (瞬时极性法)

1. 在输入端上加一个瞬时的极性$\oplus$，当然也可以加瞬时负
2. 根据各种元件的原则，推出输出量是正瞬时极性还是负瞬时极性，并把它作为一个信号源
3. 看输入端是否有一个关于输出量的响应
4. 若响应是增强了输入端信号的变化，则为正反馈；若响应是抑制了输入端信号的变化，则为负反馈

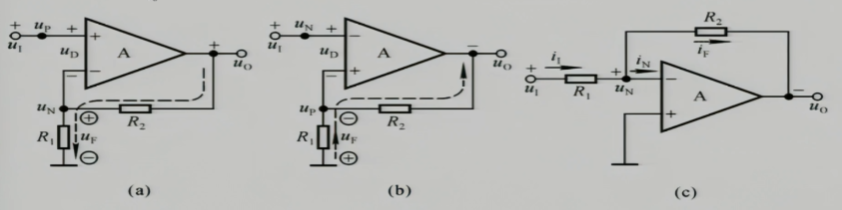
比如这三个图

反馈信号与输入信号：

1. 相异端子：两个端子上的极性，如果极性相同，为负反馈，反之为正反馈
2. 相同端子：两个极性如果极性相同，为正反馈，极性相反为负反馈
   比如这个电路

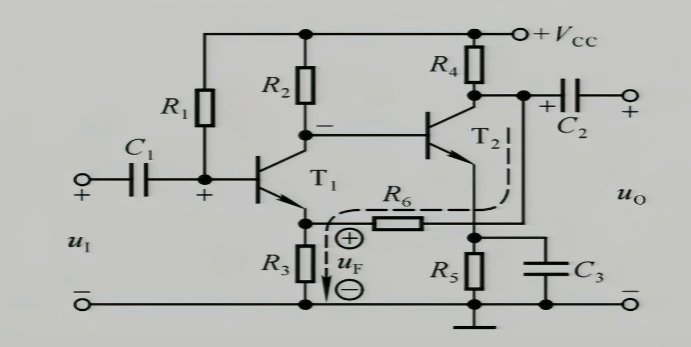
在输入加一个正极性，使得：

• $T_{1}$的发射极会有一个向下的电流增量，它导致了$T_{1}$的反相输入端口发射极 e 有一个正极性，所以在$T_{1}$这一级有一个同级的负反馈；导致$T_{2}$的基极电位有一个负极性，
• $T_{1}$的集电极会有一个向下的电流增量，它导致了$T_{2}$的基极输入有一个负极性进而导致$T_{2}$集电极上有一个向上的电流使得输出有一个正极性，并且输出与$T_{1}$的发射极相连，电流向下，导致发射极电压为正极性，这是级间的负反馈

1.2.3 交、直流反馈的判断

如果直流通路里面存在反馈，它就是直流反馈，反之为交流反馈，对于直接耦合放大电路来说，直流存在反馈，则交流一定也存在反馈

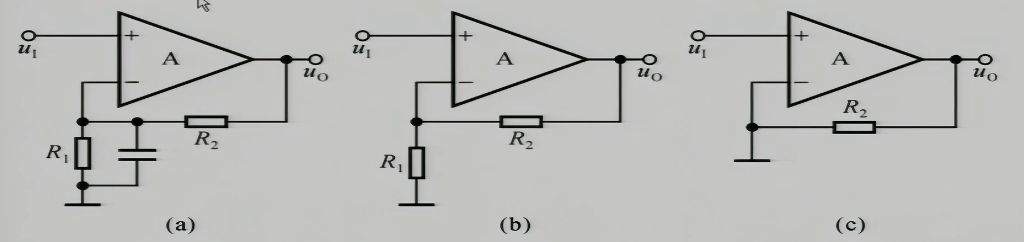
这个电路 (b) 是直流通路，(c) 是交流通路，显然直流通路下存在一个直流反馈，交流通路下无反馈

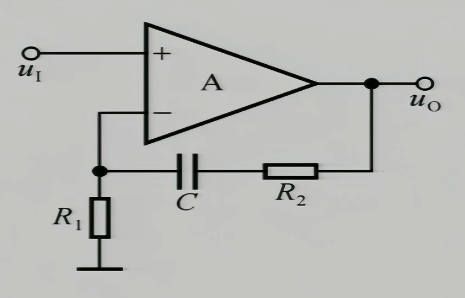
这个电路直流下不存在反馈 (电容看做断路)，交流下存在反馈

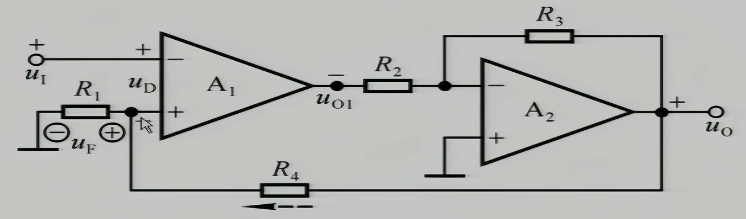
上图存在两个反馈 $T_{2}$ 到 $T_{1}$ 的负反馈，$T_{2}$ 本级的负反馈

2 负反馈放大电路的组态

以下的分析全部基于交流的、负反馈放大电路

2.1 判别

2.1.1 从输出端(电压/电流反馈)

• 电压负反馈：反馈信号取自于输出电压
• 电流负反馈：反馈信号取自于输出电流
  把输出电压$u_{0}$置零，如果反馈信号没了，那就是电压反馈，如果反馈信号还在，那就是电流反馈

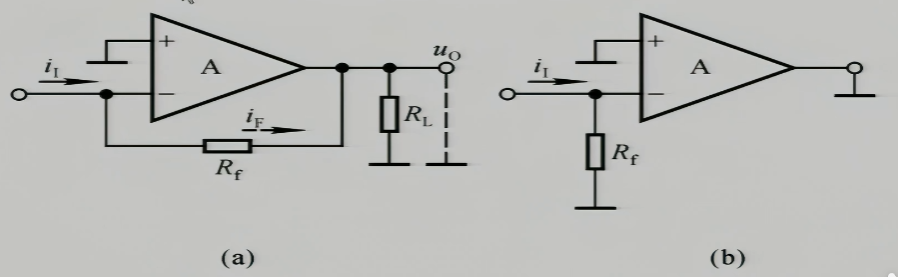
拿到手我们应该先判别有没有反馈，确定有交流负反馈之后我们再去讨论组态问题

在输入端加个正，输出端有一个负极性，这个负极性被拉回来，所以存在负反馈，再去考虑是电流负反馈还是电压负反馈的问题，我们看图(b)，把$u_{o}$置零，我们发现反馈没有了，所以这是个电压负反馈

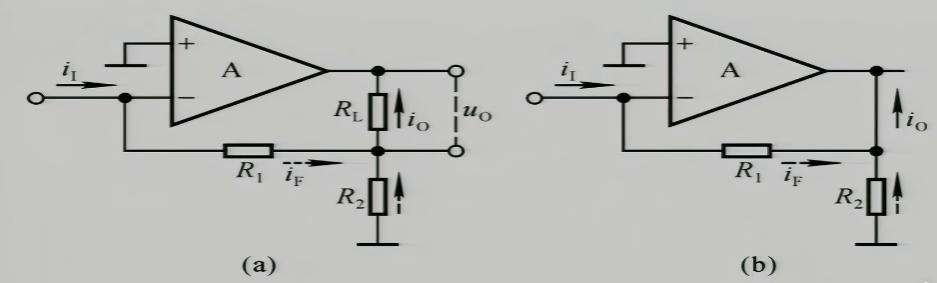
这个电路简单判断也是一个负反馈，我们把输出$R_{L}$断路，就成了(b)图，再分析(b)图，显然，反馈仍然存在，所以这是一个电流负反馈

2.1.2 串、并联反馈

反应的是输入信号和反馈信号的叠加方式，反馈信号和输入信号一定是相同的信号形式，当两个电压叠加的时候就是串联叠加，电流叠加的时候就是并联叠加

其实很简单，看输入端上反馈信号和输入信号是不是在同一个端子上，如果在不同的端子上就是串联反馈，如果在相同的端子上就是并联反馈

2.2 四种组态

2.2.1 电压串联负反馈电路

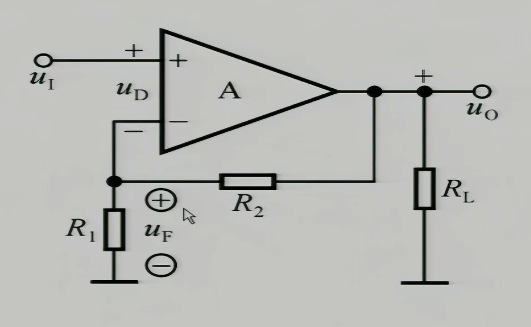
我们通过前面的方法，首先这是一个负反馈，并且输入信号和输出信号不在同一个端子上，所以是个串联负反馈，再通过把$u_{o}$接地置零，判断出他是一个电压串联负反馈电路

我们来分析这个反馈电路是稳定什么的，若$R_{L}$负载电阻减小，则输出电压想要减小，输出电压一旦减小，必然引起反向输入端$u_{N}$的减小，进而导致$u_{D}$变大，导致输出电压$u_{o}$变大从而不减小，同理$u_{o}$也不增大，即它稳定的输出电压，造就了一个电压信号源

2.2.2 电流串联负反馈电路

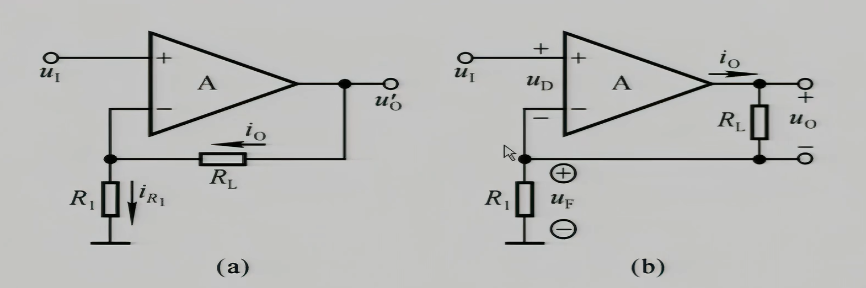
首先这是一个负反馈，而且输入和输出信号不在同一个端子上，所以是个串联负反馈，再通过把$u_{o}$置零短接后，回路依然存在，$R_{1}$的分压作用仍然存在，反馈仍然存在，所以这是个电流串联负反馈电路

我们再来分析它来稳定输出什么，若$R_{L}$减小，则$i_{O}$就想增大，导致$R_{1}$上的电流变大，它的分压变大，导致$u_{N}$增大，$u_{D}$减小，使得$i_{O}$又减小，稳定了$i_{O}$，反之同理，即它稳定的输出电流，造就了一个电流信号源，并且他把电压信号转换为电流信号进行输出

2.2.3 电压并联负反馈电路

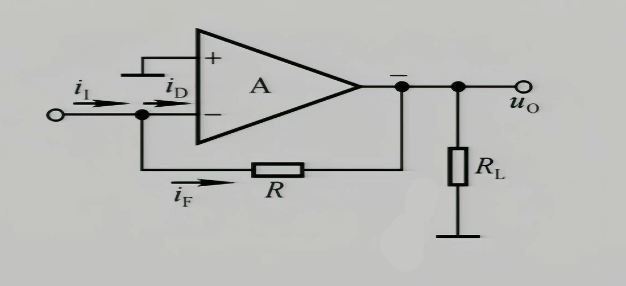
这是个电压并联负反馈电路

它实现了把电流信号转换为电压信号进行输出，用于稳定电压

2.2.4 电流并联负反馈电路

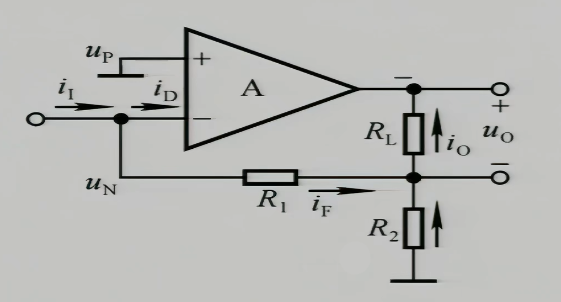
这是电流并联负反馈电路

即它稳定的输出电流，造就了一个电流信号源

3 负反馈放大电路的方块图及一般表达式

深度负反馈：可以不用关心运放内部电路，放大倍数几乎只由外部的反馈电路来决定
我们需要知道一个反馈电路什么时候进入深度负反馈，并且会给我们的电路带来怎么样一个影响，所以我们设计了负反馈放大电路的框图

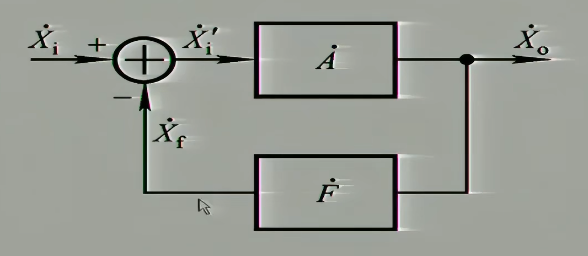
• $\dot{A}$：开环的基本放大电路(开环放大倍数)
• $\dot{F}$：反馈网络(反馈系数)
• $\dot{X_{i}}$：输入量
• $\dot{X_{f}}$：反馈量
• $\dot{X_{i}}’$：净输入量
• $\dot{X_{o}}$：输出量

3.1 各量的关系

• $\dot{X_{o}}=\dot{A}\dot{X_{i}}$
• $\dot{X_{f}}=\dot{F}\dot{X_{o}}$
• $\dot{X_{i}}’=\dot{X_{i}}-\dot{X_{f}}$

3.1.1 闭环放大倍数

如果我想获得输入量$\dot{X_{i}}$和输出量$\dot{X_{o}}$的关系就要把中间的电路等效为一个闭环放大倍数

$$\dot{A_{f}}=\frac{\dot{X_{o}}}{\dot{X_{i}}}=\frac{\dot{A}\dot{X_{i}}}{\dot{X_{i}}’+\dot{F}\dot{A}\dot{x_{i}}}=\frac{\dot{A}}{1+\dot{A}\dot{F}}$$

其中$\dot{A}\dot{F}$表明了$\dot{X_{i}}’$和$\dot{X_{f}}$的关系，我们把它定义为环路放大倍数

3.1.2 环路放大倍数

表明了我净输入量进入反馈电路过了一圈之后变成反馈量的系数，是反馈量和净输入量的关系

$$\dot{A}\dot{F}=\frac{\dot{X_{f}}}{\dot{X_{i}}’}$$

3.1.3 反馈深度

$|1+\dot{A}\dot{F}|$是反馈深度，当$|1+\dot{A}\dot{F}| \gg1$时，我们叫这个反馈电路状态为深度负反馈，在深度负反馈下，电路的$\dot{A}$非常非常大

3.1.4 深度负反馈下的$\dot{A_{f}}$

当电路为深度负反馈时，因为$\dot{A}$非常非常大

$$
\dot{A_{f}}=\frac{\dot{A}}{1+\dot{A}\dot{F}}\approx\frac{1}{\dot{F}}
$$

它的意义：$\dot{A}$实际上很不稳定，受外界的影响它会上下波动，但如果深度负反馈，$\dot{A_{f}}$几乎与$\dot{A}$无关，只与$\dot{F}$有关，而反馈网络一般是由电阻等元件构成所以相对更稳定，并且$\dot{A}$太大了，如果没有反馈运放很容易就超出了线性区，压根没法用

3.1.5 高频时的$\dot{X_{i}}$

我们知道

$$
\dot{X_{i}=}\dot{X_{i}}-\dot{A}\dot{F}\dot{X_{i}}’
$$

以上的量全部为相量，但当信号频率处于中频段的时候，上式可以近似看成

$$
|\dot{X_{i}}’|=|\dot{X_{i}}|-|\dot{A}\dot{F}\dot{X_{i}}’|
$$

但我们把信号从中频段移到高频，由于相移，一旦相移到$180\degree$时，上式就会变成

$$
|\dot{X_{i}}’|=|\dot{X_{i}}|+|\dot{A}\dot{F}\dot{X_{i}}’|
$$

就会产生类似正反馈中自激振荡的效果

3.2 四种组态电路的方块图

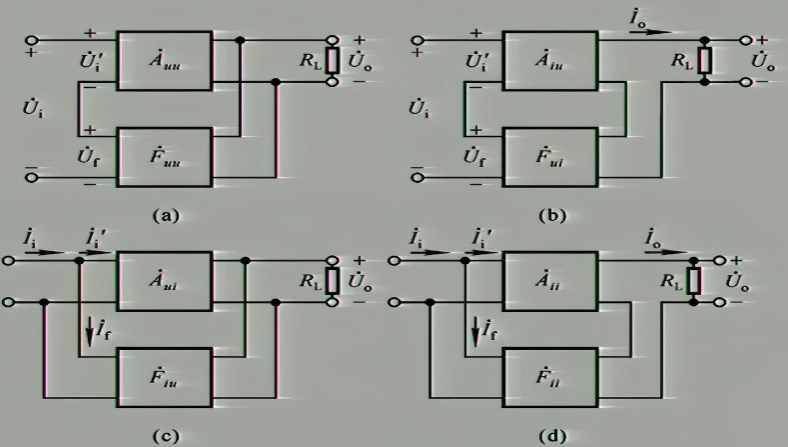
这个图把四种组态的特点表现的淋漓尽致：

• (a)：电压串联负反馈电路，输入是电压信号，以串联的方式叠加，反馈量从电压信号取来，并输出稳定电压信号

$$
\dot{U_{i}}\quad\dot{U_{i}}’\quad \dot{U_{f}}\quad \dot{U_{o}}
$$

$$
\dot{A}_{uu}=\frac{\dot{U_{o}}}{\dot{U}_{i}’}\quad \dot{F}_{uu}=\frac{\dot{U_{f}}}{\dot{U}_{o}}
$$

$$
\dot{A}_{uuf}=\frac{\dot{U}_{o}}{\dot{U}_{i}}=\frac{\dot{A}_{uu}}{1+\dot{A}_{uu}\cdot \dot{F}_{uu}}=\frac{1}{\dot{F}_{uu}}
$$

• (b)：电流串联负反馈电路，输入是电压信号，以串联的方式叠加，反馈量从电流信号取来，并输出稳定电流信号，把电压信号转变成了电流信号

$$
\dot{U_{i}}\quad\dot{U_{i}}’\quad \dot{U}_{f}\quad \dot{U_{o}}\quad \dot{I_{o}}
$$

$$
\dot{A}_{iu}=\frac{\dot{I_{o}}}{\dot{U}_{i}’}\quad \dot{F}_{ui}=\frac{\dot{U_{f}}}{\dot{I}_{o}}
$$

$$
\dot{A}_{iuf}=\frac{\dot{I}_{o}}{\dot{U}_{i}}=\frac{1}{\dot{F}_{ui}}\quad \dot{A}_{uuf}=\dot{A}_{iuf}\cdot R_{L}
$$

• (c)：电压并联负反馈电路，输入是电流信号，以并联的方式叠加，反馈量从电压信号取来，并输出稳定电压信号，把电流信号转变为了电压信号

$$
\dot{I_{i}}\quad\dot{I_{i}}’\quad \dot{I_{f}}\quad \dot{U_{o}}
$$

$$
\dot{A}_{ui}=\frac{\dot{U_{o}}}{\dot{I}_{i}’}\quad \dot{F}_{iu}=\frac{\dot{I_{f}}}{\dot{U}_{o}}
$$

$$
\dot{A}_{uif}=\frac{\dot{U}_{o}}{\dot{I}_{i}}=\frac{1}{\dot{F}_{iu}}
$$

• (d)：电流并联负反馈电路，输入是电流信号，以并联的方式叠加，反馈量从电流信号取来，并输出稳定电流信号

$$
\dot{I_{i}}\quad\dot{I_{i}}’\quad \dot{I_{f}}\quad \dot{I_{o}}
$$

$$
\dot{A}_{ii}=\frac{\dot{I_{o}}}{\dot{I}_{i}’}\quad \dot{F}_{ii}=\frac{\dot{I_{f}}}{\dot{I}_{o}}
$$

$$
\dot{A}_{iif}=\frac{\dot{I}_{o}}{\dot{I}_{i}}=\frac{1}{\dot{F}_{ii}}
$$

4 深度负反馈的实质与放大倍数的分析

4.1 深度负反馈的实质

实际上我们根据前面的分析，大概能感觉到其实深度负反馈的实质就是忽略了净输入量，其实就是虚短(两个输入端之间相当于短路，导致净输入量为0)，使得闭环放大系数等于反馈系数的倒数

并且它实际上提升了一层抽象，我们不再需要关心集成运放里那三层复杂的电路，我们只需要设计好外部的反馈电路就能控制运放的工作

4.2 放大倍数的分析

4.2.1 步骤

1. 判别组态，找出反馈网络(能体现反馈量和输出量之间的关系的网络)
2. 算出$\dot{F}$
3. 算出$\dot{A}_{f}=\frac{1}{\dot{F}}$
4. 把$\dot{A}_{f}$转成$\dot{A}_{uuf}$

4.2.2 各种组态的分析

4.2.2.1 电压串联负反馈

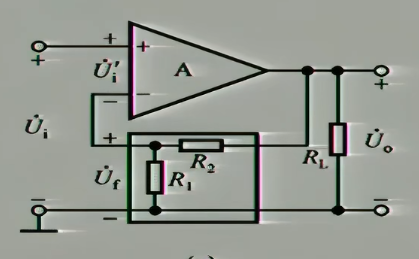
显然反馈网络是方框框的部分首先计算$\dot{F}$

$$
\dot{F}_{uu}=\frac{\dot{U}_{f}}{\dot{U}_{o}}=\frac{R_{1}}{R_{1}+R_{2}}
$$

所以闭环放大倍数为：

$$
\dot{A}_{uuf}=\frac{R_{1}+R_{2}}{r_{1}}=\frac{\dot{U}_{o}}{\dot{U}_{i}}
$$

$$
\dot{U}_{0}=\frac{R_{1}+R_{2}}{R_{1}}\cdot \dot{U}_{i}
$$

上面这个式子相当于$y=kx$，实现了一个比例放大，运算的功能开始了

4.2.2.2 电流串联负反馈

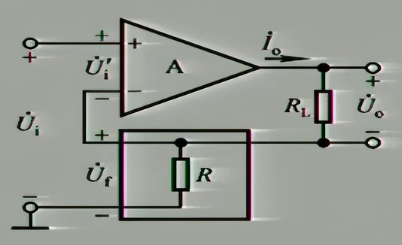
首先计算$\dot{F}$

$$
\dot{F}_{ui}=\frac{\dot{U}_{f}}{\dot{I}_{o}}=R
$$

闭环放大倍数：

$$
\dot{A}_{iuf}=\frac{1}{R}=\frac{\dot{I}_{o}}{\dot{U}_{i}}
$$

$$
\dot{I}_{o}=\frac{\dot{U}_{i}}{R}
$$

上面的式子把一个电压转换为电流

$$
\dot{A}_{uuf}=\frac{\dot{U}_{o}}{\dot{U}_{i}}=\frac{R_{L}}{R}
$$

即

$$
\dot{U}_{o}=\frac{R_{L}}{R}\cdot\dot{U}_{i}
$$

因为有$R_{L}$的存在，它的输出电压与$R_{L}$相关，所以它和电压串联不同，它不是一个电压源

4.2.2.3 电压并联负反馈

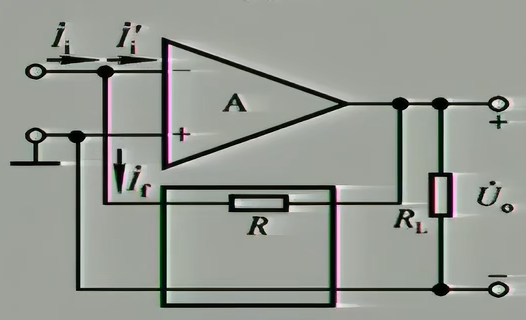
首先计算$\dot{F}$

$$

\dot{F}{iu}=\frac{\dot{I}{f}}{\dot{U}{o}}=\frac{-\frac{\dot{U}{o}}{R_{f}}}{\dot{U}{o}}=-\frac{1}{R{f}}

$$

再计算闭环放大倍数

$$
\dot{A}_{uif}=\frac{\dot{U}_{o}}{\dot{I}_{i}}=-R_{f}
$$

$$
\dot{U}_{o}=-R_{F}\cdot \dot{I}_{i}
$$

上面的式子是把电流信号转换为电压信号

如果我想获得电压放大倍数呢，我们把它前端的输出看为一个有内阻的电流源或者电压源

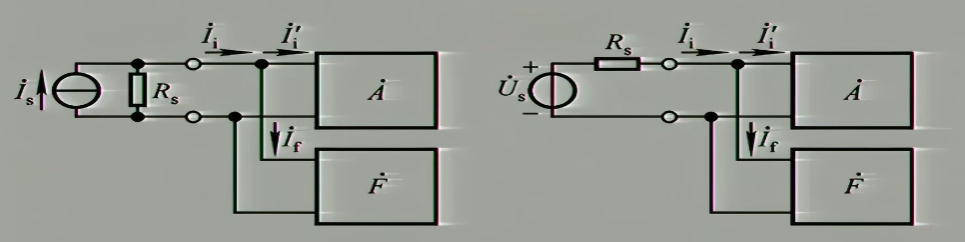
$$
\dot{A}_{usf}=\frac{\dot{U}_{o}}{-\dot{U}_{s}}=\frac{\dot{U}_{o}}{\dot{I}_{i}\cdot R_{S}}=-\frac{R_{f}}{R_{S}}
$$

4.2.2.4 电流并联负反馈

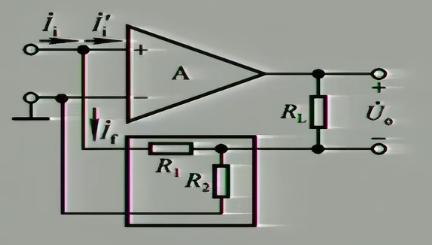
首先计算$\dot{F}$

$$

\dot{F}{ii}=\frac{\dot{I}{f}}{\dot{I}{o}}=\frac{-\frac{R{2}}{R_{1}+R_{2}}\cdot \dot{I}{o}}{\dot{I}{o}}=-\frac{R_{2}}{R_{1}+R_{2}}

$$

再计算闭环放大倍数

$$
\dot{A}_{iif}=\frac{\dot{I}_{o}}{\dot{I}_{i}}=-\frac{R_{1}+R_{2}}{R_{2}}
$$

$$
\dot{I}_{o}=-\frac{R_{1}+R_{2}}{R_{2}}\cdot \dot{I}_{i}
$$

上式完成了一个电流的比例放大

5 负反馈对放大电路性能的影响

5.1 稳定放大倍数

在中频段的时候，

$$
A_{f}=\frac{A}{1+AF}
$$

如何证明闭环放大倍数提高？

若出现一个外界扰动导致出现一个$\Delta A$和$\Delta A_{f}$的变化，如果我们要证明闭环放大倍数提高，用$\frac{\Delta A}{A}$和$\frac{\Delta A_{f}}{A_{f}}$比较，看是否后者比前者小，即出现的变化小，稳定放大倍数

$$
\begin{align}
\mathrm{d}A_{f}&=\frac{(1+AF)\cdot \mathrm{d}A-AF\cdot \mathrm{d}A}{(1+AF)^{2}} \\
&=\frac{\mathrm{d}A}{(1+AF)^{2}}
\end{align}
$$

$$
\therefore
\begin{align}
\frac{\mathrm{d}A_{f}}{\frac{A}{1+AF}}&=\frac{\frac{\mathrm{d}A}{A}}{\frac{(1+AF)^{2}}{A}}\cdot \frac{1+AF}{A} \\
\frac{\mathrm{d}A_{F}}{A_{f}}&=\frac{1}{1+AF}\cdot \frac{\mathrm{d}A}{A}
\end{align}
$$

即稳定度提高了，提高了$\frac{1}{1+AF}$倍，$1+AF$这个数值之前被我们定义为反馈深度

5.2 改变输入/输出电阻

5.2.1 对输入电阻

5.2.1.1 串联

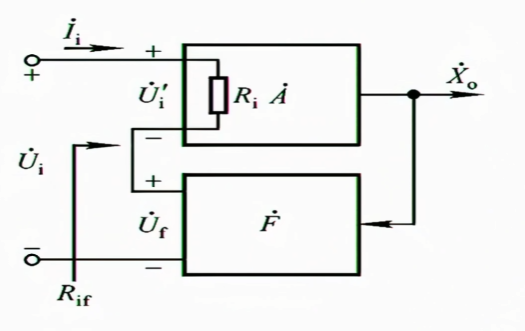
如图，之前的输入电阻是$R_{i}$，现在在深度负反馈状态下，我们等效出一个输入电阻$R_{if}$，则深度负反馈对输入电阻的作用就是$R_{f}$和$R_{if}$之间的关系

$$
R_{if}=\frac{\dot{U}_{i}}{\dot{I}_{i}}=\frac{\dot{U}_{i}’+\dot{A}\dot{F}\dot{U}_{i}’}{\dot{I}_{i}}
$$

又$R_{i}=\frac{\dot{U}_{i}’}{\dot{I}_{i}}$

$$
\therefore(1+\dot{A}\dot{F})R_{i}=R_{if}
$$

即输入电阻被提高了$1+\dot{A}\dot{F}$倍，即被提高了反馈深度倍

5.2.1.2 并联

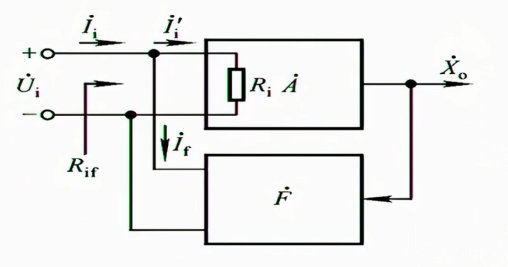
如图，之前的输入电阻是$R_{i}$，现在在深度负反馈状态下，我们等效出一个输入电阻$R_{if}$，则深度负反馈对输入电阻的作用就是$R_{f}$和$R_{if}$之间的关系

$$
R_{if}=\frac{\dot{U}_{i}}{\dot{I}_{i}}=\frac{\dot{U}_{i}}{(1+\dot{A}\dot{F})\dot{I}_{i}’}=\frac{R_{i}}{1+\dot{A}\dot{F}}
$$

即并联反馈下输入电阻变成原来的$\frac{1}{1+\dot{A}\dot{F}}$，即被降低了反馈深度倍

5.2.2 对输出电阻

5.2.2.1 电压

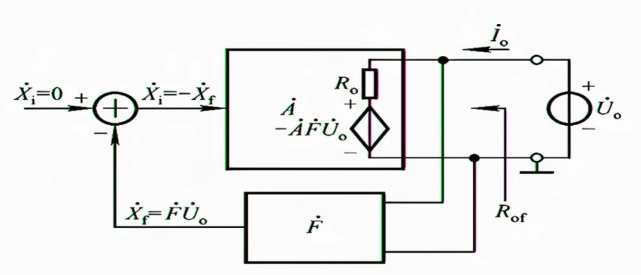
对于负载我们通过一些操作把负载效益等效掉，以简化问题的复杂程度

$$
R_{of}=\frac{\dot{U}_{o}}{\dot{I}_{o}}
$$

由图

$$
\dot{U}_{o}=-\dot{A}\dot{F}\dot{U}_{o}+R_{o}\cdot \dot{I}_{o}
$$

$$
\therefore R_{of}=\frac{R_{o}}{1+\dot{A}\dot{F}}
$$

即电压反馈下输出电阻会变成原来的$\frac{1}{1+\dot{A}\dot{F}}$，这意味着我们能真正造出接近理想电压源的极小内阻的电压源

5.2.2.2 电流

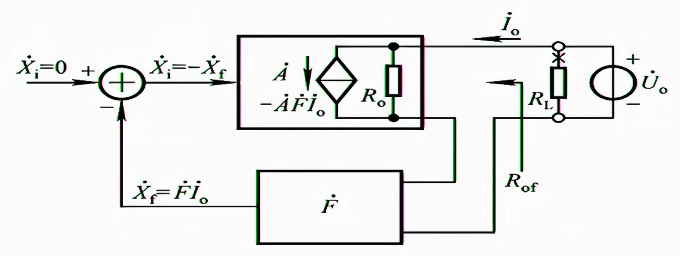
$$
R_{of}=(1+\dot{A}\dot{F})R_{o}
$$

即电流反馈下输出电阻会变成原来的$1+\dot{A}\dot{F}$倍，这意味着我们能真正的造出接近理想电流源的内阻极大的电流源

5.3 展宽频带

使通频带展宽$1+AF$倍

5.3.1 减小非线性失真

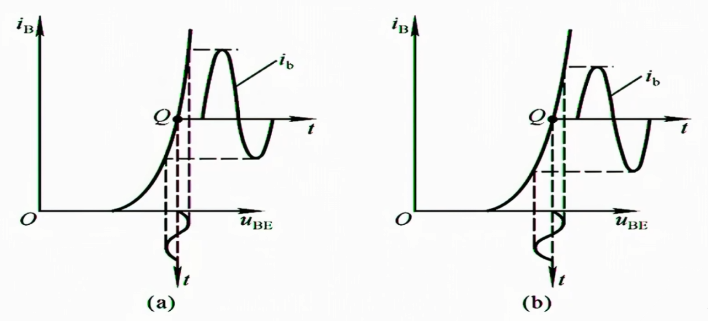
图(a)中上半轴很大，下半轴很小，当我用他引回一个反馈的时候，它会导致我的$i_{B}$输入也呈现这样一个类似的形状，从而进行抵消使得$i_{b}$输出长得更好看

6 负反馈对放大电路的稳定性

以后再补，记得提醒我