本系列笔记仅为个人备忘记录,若要获得最大学习效果仍建议学习郑益慧老师课程:
郑益慧老师课程
如有谬误、补充,还望不吝指正
在上一部分我们已经把先静态再动态的思想已经说的比较清楚了,后面就是使用这个思想去解决各种问题,分析各种电路
1 基本共射放大电路的动态分析
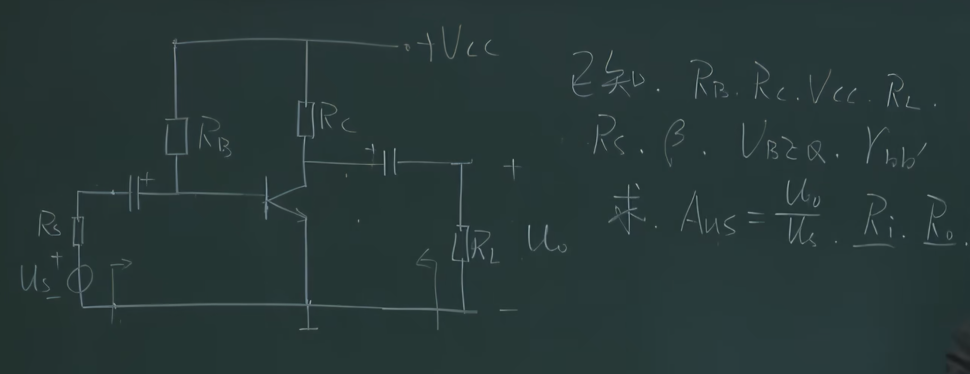
1.1 求解静态
1.1.1 直流通路
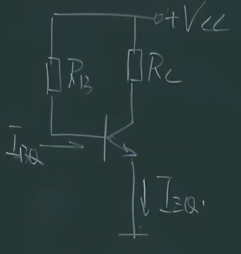
把交流置零,电容看做断路,得到直流通路
首先判断三极管是否处于放大状态下,若为放大状态,此时可以求出静态工作下的电流$I_{BQ}$和$I_{EQ}$
从地(零电位点往上看),使用电位分析法,一个元件一个元件的看,可以列出方程
$$V_{CC}=U_{BEQ}+I_{BQ}\cdot R_{B}$$
于是就可以求出$I_{BQ}$,$\therefore I_{EQ}=(1+\beta)I_{BQ},I_{CQ}=\beta I_{BQ}$
就可以计算出此时静态工作点的动态电阻
$$r_{be}=r_{bb’}+(1+\beta)\frac{V_{T}}{I_{EQ}}$$
直流的使命到此结束
1.2 求解动态
1.2.1 交流通路
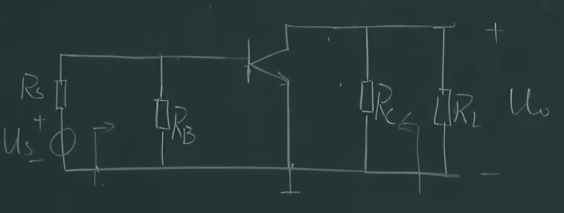
置零直流,电容看做短路,画出交流通路
1.2.2 H参数等效
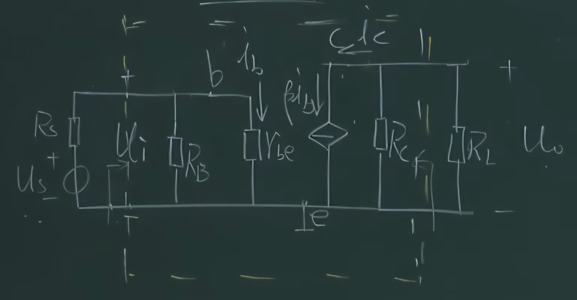
把基极到发射极换成动态电阻$r_{be}$,把集电极到发射极换成流控电流源$\beta i_{b}$,画出简化的H参数等效
此时可以算出放大电路的放大倍数
$$A_{u}=\frac{u_{o}}{u_{i}}=\frac{-i_{c}\cdot R_{L}\verb|//|R_{C}}{i_{b}\cdot r_{be}}=\frac{-\beta R_{L}\verb|//|R_{C}}{r_{be}}$$
于是我们得到了$u_{o}$和$u_{i}$的关系,如果我们再能知道$u_{s}$与$u_{i}$的关系,我们就可以得到$u_{s}$和$u_{o}$的关系,如何知道$u_{s}$与$u_{i}$的关系呢,我们从前端往后看,可以认为后面就是一个电阻$R_{i}$
此时$R_{i}=R_{B}\verb|//|r_{be}$,注意此时计算$R_{i}$也要考虑后面的负载$R_{L}$(火车头拉货的道理)
一旦我们知道了$R_{i}$,则我们可以很轻松的得出
$$\frac{u_{i}}{u_{s}}=\frac{R_{i}}{R_{i}+R_{s}}$$
于是
$$A_{us}=\frac{u_{o}}{u_{i}}\cdot \frac{u_{i}}{u_{s}}=A_{u}\cdot\frac{R_{i}}{R_{i}+R_{s}}$$
现在我们考虑$R_{o}$,$R_{o}$实际上是站在后端把前端的电路用戴维南等效电路等效出的内阻,在这个电路下$R_{o}=R_{c}$,$R_{c}$越大越能稳定输出电流,$R_{c}$越小越能稳定输出电压
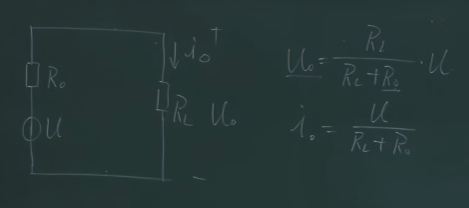
2 Q点稳定的放大电路
2.1 必要性
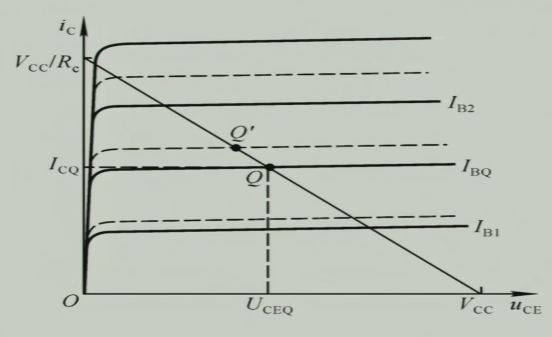
如图所示,由于温度的变化,三极管的输出特性曲线会有相对较大的变化,就会对放大电路产生影响,导致静态工作点位置的变化,就有可能导致放大的失真
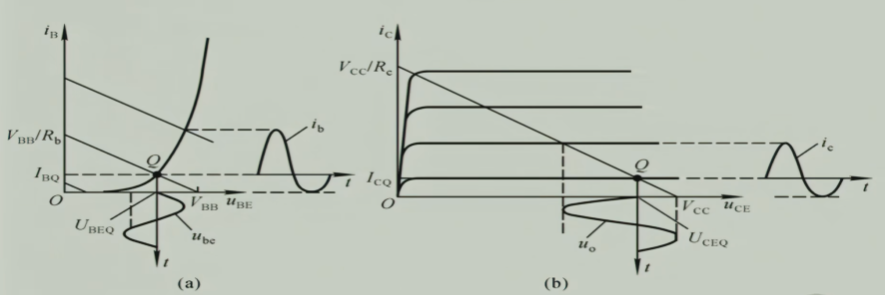
如图,静态工作点原本在放大区工作,但由于温度的变化导致它进入了截止区,这就导致了放大电路出现了截止失真
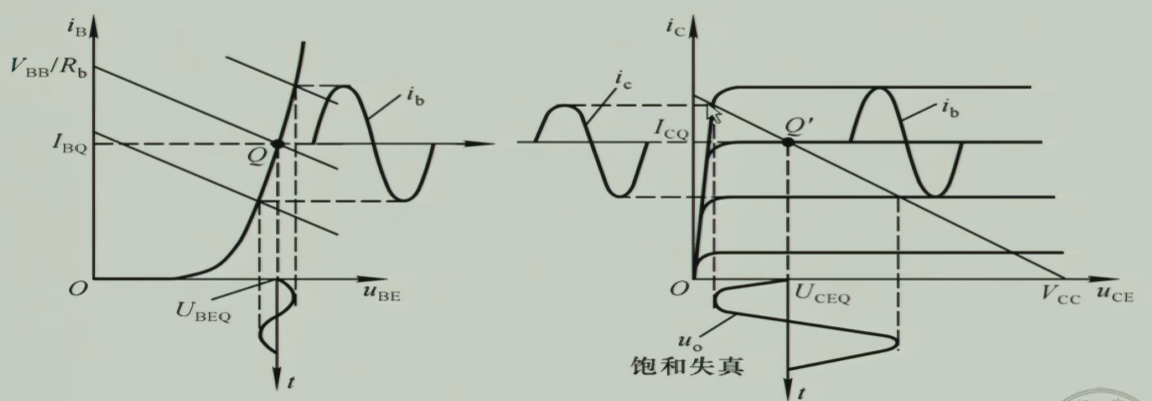
如图,静态工作点原本在放大区工作,但由于温度的变化导致输出负载线进入了饱和区,这就导致了对于某一部分的$i_{b}$放大电路根本没有能力放大,放大电路出现了饱和失真
2.1.1 对Q点影响的因素
- 温度:需要通过电路结构的方法来控制
- $V_{CC}$电源的波动:可以通过使用较好的电源来解决
- 元器件的老化:可以通过元器件出厂时预老化来稳定元器件的性能
2.2 稳定Q点的思路
2.2.1 Q点稳定的电路
2.2.1.1 构成
目前温度的升高会导致$i_{c}$值上升,而我们的目的是温度变化$i_{c}$不变,所以我们要思考是否可以引入一个东西,它的存在导致温度上升$i_{c}$下降,从而抵消掉$i_{c}$的变化
于是想到如果在温度上升时,$u_{BE}$下降进而导致$i_{B}$下降,就可以达成这种效果,于是设计出了如下电路
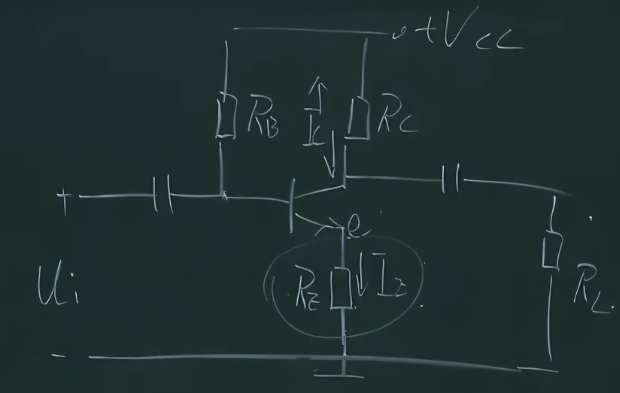
其工作原理是
$$T\uparrow\to T_{c}\uparrow\to I_{E}\uparrow\to U_{E}\uparrow\to U_{BE}\downarrow\to I_{B}\downarrow\to I_{C}\downarrow$$
但是此时这个下降效果并不保险,因为$U_{B}$也在变化,$U_{E}$的升高并不一定会使$U_{BE}$降低,所以我们使用电阻分压式稳压电路来对前端的$U_{B}$稳压
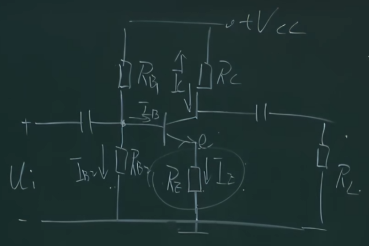
于是就构成了一个静态工作点稳定的放大电路
2.2.1.2 分析
2.2.1.2.1 直流通路
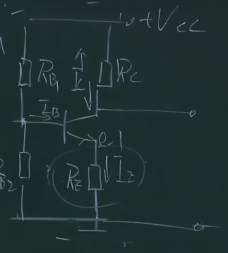
对左边$R_{B1}$和$R_{B2}$并联的部分做戴维南等效,得
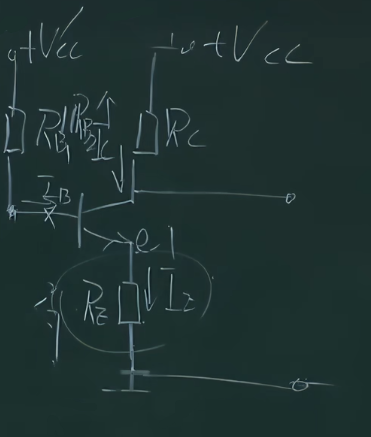
此时$V_{CC}’=\frac{R_{B2}}{R_{B1}+R_{B2}}V_{CC}$,于是就可以继续使用电位分析法计算静态工作点了
$$V_{CC}’=I_{EQ}\cdot R_{E}+V_{BEQ}+I_{BQ}\cdot R_{B1}\verb|//|R_{B2}$$
2.2.1.2.2 交流通路
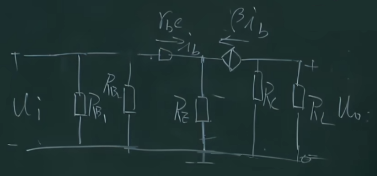
$$A_{u}=\frac{-\beta i_{b}\cdot R_{c}\verb|//|R_{L}}{(1+\beta)i_{b}\cdot R_{E}+i_{b}\cdot r_{be}}$$
于是我们就发现了一个问题,如果通过加$R_{e}$的方式实现Q点稳定,$R_{e}$会影响放大倍数,这是我们不愿看到的,所以我们可以在$R_{e}$两端并联一个电容$C_{e}$,这样在直流下$R_{e}$稳定静态工作点的作用仍然存在,但交流就可以越过$R_{e}$传导,相当于把$R_{e}$断路,使得$R_{e}$可以不影响放大倍数
于是我们就得到了静态工作点稳定的放大电路(仅阻容式耦合可以这么干)
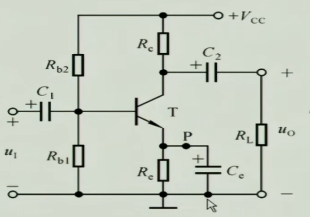
其缺点是不能集成,因为有三个硕大的电解电容,那有没有不用电容就能把$R_{e}$消灭掉的方法呢?有的,将在模电复习笔记-第六节-模拟集成电路中说到的差分放大电路
3 基本共集放大电路
前面叙述的大部分都是基本共射放大电路,当然我们也可以共集电极来搭建放大电路
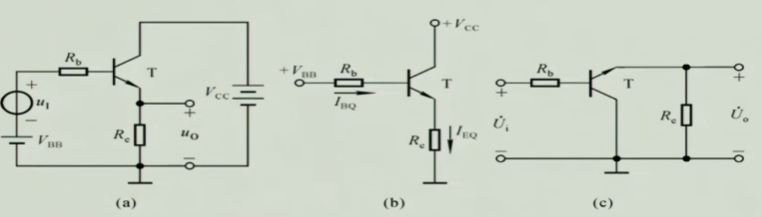
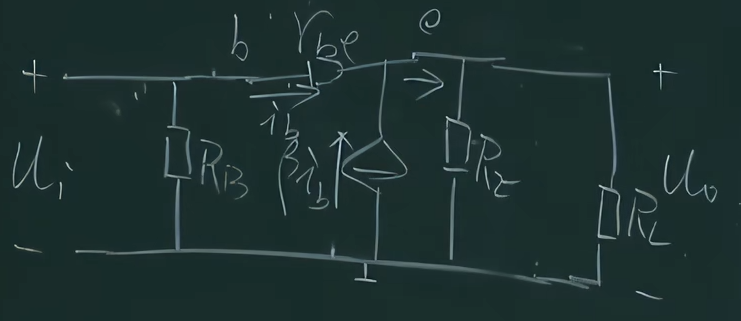
$$A_{u}=\frac{u_{o}}{u_{i}}=\frac{(1+\beta)i_{b}\cdot R_{E}\verb|//|R_{L}}{(1+\beta)i_{b}\cdot R_{E}\verb|//|R_{L}+i_{b}\cdot r_{be}}$$
也就是说这个放大倍数$A_{u}<1$,趋近于1,也就是说这个电路在电压上没放大,也不太缩小,所以我们叫他射级输出器,也叫射级跟随器,但是其实它也在放大,因为他输出的电流从$i_{b}$变成了$i_{e}=(1+\beta)i_{b}$,电流得到了放大
它的输入电阻为比较大,输出电阻比较小,这意味着它适宜接电压源输入,并且输出的电压稳定性非常好
4 基本共基放大电路
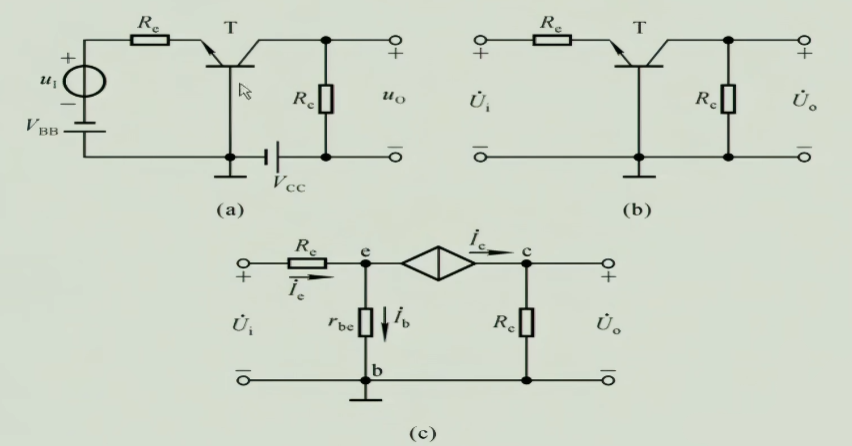
很显然,共基放大电路输入是$i_{e}$,输出是$i_{c}$,所以他一定不会放大电压
$$A_{u}=\frac{\beta i_{b}\cdot R_{c}\verb
|//|R_{L}}{i_{b}\cdot r_{be}+(1+\beta)i_{b}\cdot R_{e}}$$
一般来说这种电路$R_{e}$很小,它有很好的频率特性,同频带较宽,是共射的$1+\beta$倍,它的输入电阻很小,输出电阻
5 晶体管放大电路的派生电路
5.1 复合管放大电路
5.1.1 复合管的组成
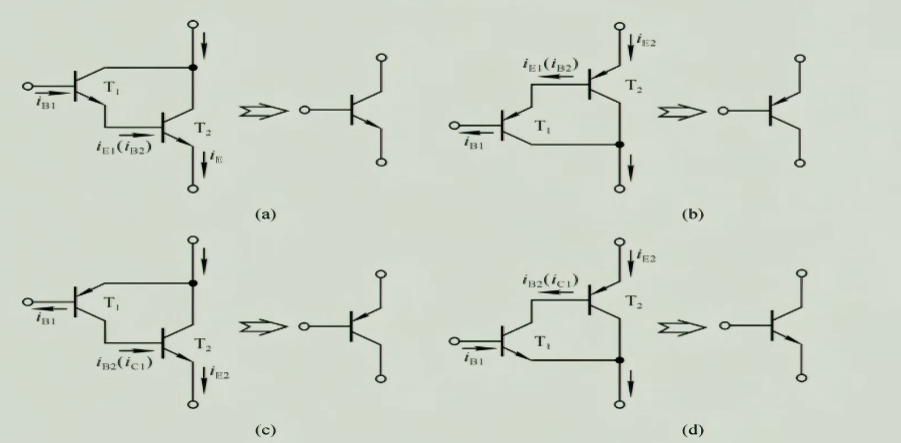
这种复合的结构叫做达林顿结构,这种复合管叫做达林顿管
这样的结构意味着等效出的整个管子的放大倍数$\beta=\beta_{1}\cdot \beta_{2}$
5.1.2 复合管构成的电路
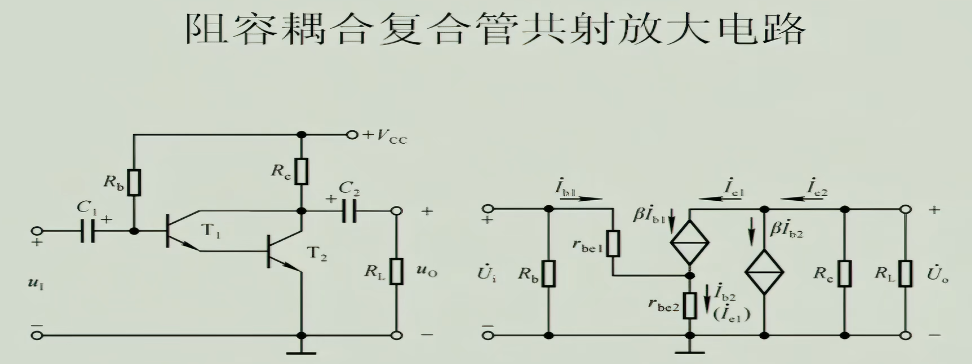
5.2 共射-共基放大电路
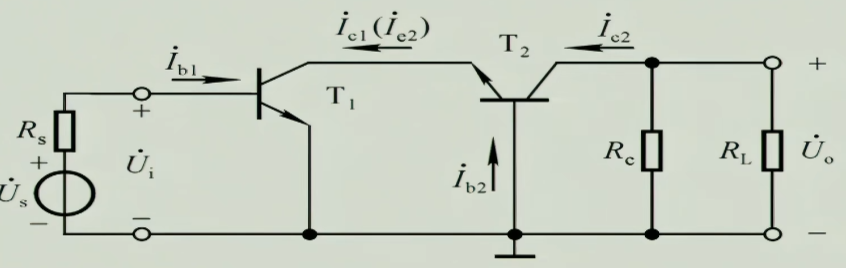
它集合了两种放大电路的优点,先使用共射放大电路把电流放大,再使用共基放大电路放大电压并且利用共基通频带宽来使整个电路通频带拓宽
5.3 共集-共基放大电路
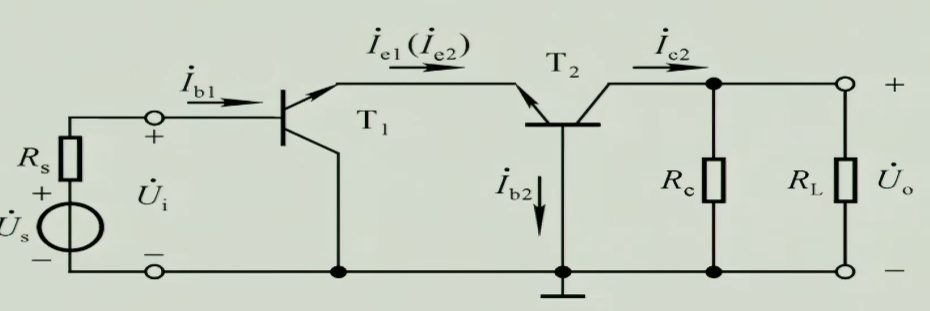
使用了共集输入电阻大的特点,适合用于接电压源去和电压源抢信号
有如此之多的放大电路,把每个电路的静态和动态通路都记住背过显然不现实也没必要,所以我们要掌握它的分析方法,掌握三极管的使用,才能一法通,万法通