本文最后更新于 189 天前，如有失效或谬误请评论区留言。

本系列笔记仅为个人备忘记录，若要获得最大学习效果仍建议学习郑益慧老师课程：
郑益慧老师课程
如有谬误、补充，还望不吝指正

前情提要（绪论）

1 本征半导体与杂质半导体

1.1 半导体

1.1.1 概念

导电能力介于导体和绝缘体的材料

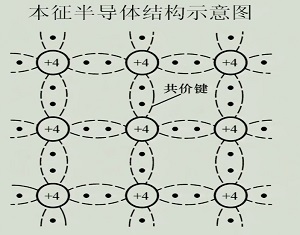
1.1.2 本征半导体

是一种纯净的、具有晶体结构的半导体

其晶体结构如下图所示

1.2 载流子

本征半导体的各种组成粒子中，共价键里的价电子无法导电，但是它作为半导体具有一些导电的性质，则一定有某些粒子作为载流子，本征激发和复合的速度和温度决定了载流子的浓度，载流子的浓度决定了本征半导体的导电能力

1.2.1 本征激发

因为粒子热运动$\to$使电子有机会逃出共价键的束缚，成为自由电子，并留下一个空穴，如图所示

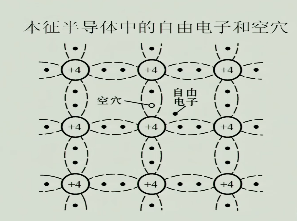
自由电子：带负电，可以自由移动，可以导电
空穴：带正电，可以通过电子对空穴的填补相对沿电场方向移动，也可以导电
本征激发越多，导电能力越好

1.2.2 复合

自由电子在移动过程中撞到空穴，与空穴重新形成一个价电子的过程叫做复合

1.2.3 载流子的浓度

温度与本征激发的速度相关，温度越高本征激发的速度越快，而复合的速度与载流子浓度相关，浓度越高，复合的速度越快

温度升高，载流子的浓度升高，直到温度达到某个值后载流子浓度几乎不变，此时本征激发和复合速率相近，达到动态平衡

1.3 杂质半导体

1.3.1 概念

本征半导体并没有什么用处，半导体材料有可掺杂性，我们可以在纯净的本征半导体中扩散少量杂质元素，构成杂质半导体

1.3.2 N型半导体

在本征半导体里掺入少量五价元素(如磷)

如图所示，由于五价元素外围有五个电子，其中四个用于形成共价键，剩下的一个就成为自由电子，显著的提高了半导体的导电性

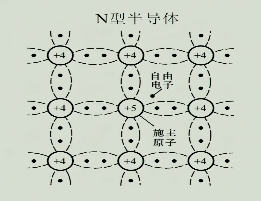
此时半导体里有两种载流子：

自由电子：分为本征激发出的自由电子和掺杂元素带来的自由电子
空穴：本征激发出的空穴
此时自由电子是多数载流子，简称多子；空穴是少数载流子，简称少子
主要导电的载流子是自由电子，自由电子带负电，所以这种半导体被称为N(Negative)型半导体

1.3.2.1 温度对N型半导体的影响

温度对N型半导体的多子影响不大，少子对温度非常敏感

1.3.3 P型半导体

在本征半导体里掺入少量三价元素(如硼)

与N型半导体类似，掺入三价元素后每个硼原子提供一个空穴，此时空穴为多子，自由电子为少子
主要导电的载流子是空穴，空穴带正电，所以这种半导体被称为P(Positive)型半导体

PN结

1 PN结的形成

当把P型半导体和N型半导体放到一起时，就发生了浪漫的变化

1.1 扩散运动

扩散运动：粒子在浓度梯度的作用下，从浓度高的地方往浓度低的地方运动
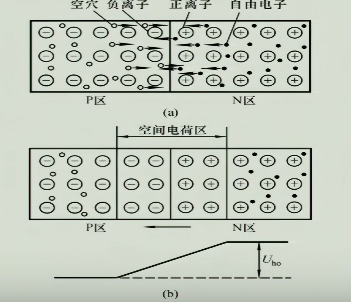
P区里空穴浓度高，N区里自由电子浓度高，他们相互扩散，在中间发生了激烈的战斗，一个电子和一个空穴一对一的湮灭

1.2 空间电荷区

随着扩散运动的进行，逐渐在中间产生了一个耗尽层(空间电荷区)，形成了一个空间电场，阻止扩散运动继续作用，这个空间电荷区又被称作 PN结

1.3 PN结形成后的扩散运动

由于粒子热运动，本身带有能量，可能出现某些粒子可以冲破中间空间电场的势垒束缚，即扩散运动会一直存在，只是会变得非常非常小

1.4 漂移运动

P区和N区不仅有多子，还有少量由本征激发出的少子，对于多子来说的势垒对少子来说可以看做一个加速场，少子只要一进入空间电荷区就会被电场推着飘到对面，这种运动称为漂移运动

2 PN结的特性

2.1 单向导电性

2.1.1 正向导通

给PN结外加正向电压(P接正，N接负)，如图所示

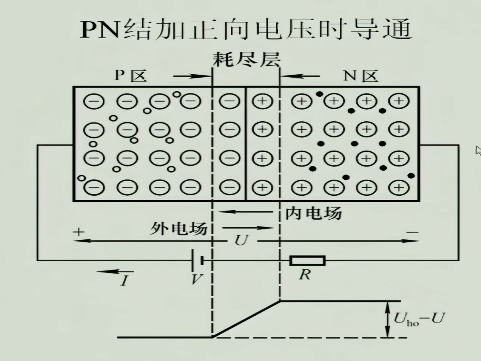
此时外电场和内电场方向相反，外电场在削弱内电场的作用，相当于外加电场在削弱空间电荷区势垒的高度，使得多子更容易通过势垒，扩散运动得以恢复，电流迅速增大

2.1.2 反向截止

给PN结外加反向电压(P接负，N接正)，如图所示

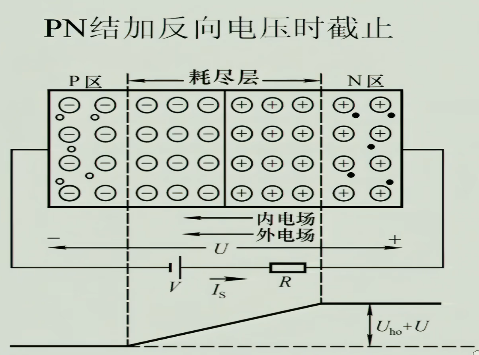
此时外电场和内电场方向相同，外电场增强内电场的作用，使得PN结越来越厚，漂移运动继续被压制，使得电流变得极小(此时漂移运动被加强，有一个微安级的电流)

2.2 伏安特性

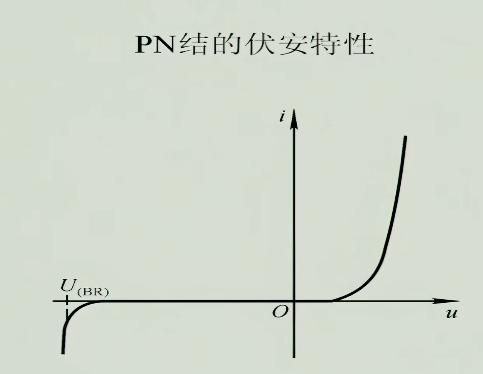
2.2.1 电流方程

$$
i=I_{s}\cdot(e^{\frac{u}{U_{T}}}-1)
$$
其中：

$I_{s}$：反向饱和电流
$U_{T}$：温度当量，把温度转化为电压值，室温下$U_{T}=26mV$
$u$：二极管上所加的电压
$u$一般情况下至少几百$mV$，而$U_{T}$只有$26mV$，这意味着$e^{\frac{u}{U_{T}}}$很大，后面的$-1$可以忽略，这个方程可以近似看做一个指数的关系

2.2.2 正向特性
死区：外电场从0开始增加到与内电场大小相同把内电场抵消掉，这个区域称为死区
导通电压：能使PN结导通的电压，称为导通电压，每种基材的PN结的导通电压不同

2.2.3 反向特性
反向饱和电流$I_{s}$：漂移运动产生的电流

2.2.3.1 反向击穿
雪崩击穿：当掺杂浓度比较低，外电场足够强的时候，PN结会变成一个粒子加速器，长度足够，场强足够，一个粒子进入PN结，不断的被加速，加速到能量足够时刚好撞到了一个共价键上，把价电子撞出去，然后继续碰撞发生了链式反应，瞬间把PN结击穿
齐纳击穿：掺杂浓度高的时候，PN结狭窄，外加电场导致PN结里场强极大，直接从共价键里把价电子拉出来，PN结击穿
温度越高，雪崩击穿要求的电压越高，齐纳击穿要求的电压越低

但此时PN结还没有损坏，PN结在击穿后损坏的真正原因是PN结反向击穿后变成一个电阻，消耗大量电功率，引起PN结温度升高，最终烧毁，称为热击穿；若击穿后温度未过高，PN结并不会损坏

当PN结在反向击穿区中时，很大的电流变换范围内其电压几乎是不变的，我们可以使用这条特性去制作稳压二极管

2.3 PN结的电容效应

2.3.1 势垒电容

在势垒区，当PN结外加电压变化时，引起积累在势垒区的空间电荷的变化，即耗尽层的电荷量随外加电压而增多或减少，这种现象与电容器的充、放电过程相同。耗尽层宽窄变化所等效的电容称为势垒电容

2.3.2 漂移电容

来自于非平衡少数载流子（简称非平衡少子）在pn结两边的中性区内的电荷存储所造成的电容效应（因为在中性扩散区内存储有等量的非平衡电子和非平衡空穴的电荷，它们的数量受到结电压控制）

半导体二极管

1 二极管的常见结构

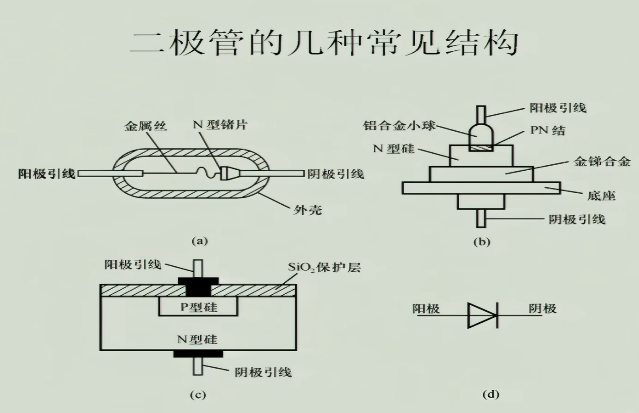
2 二极管的特性与参数

2.1 伏安特性

二极管的伏安特性与PN结几乎一致

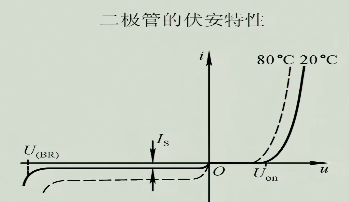
2.1.1 体电阻

二极管在通过正向电流时，内部材料所表现出来的等效电阻，称为体电阻，导致正向导通时，二极管电流比PN结小

2.1.2 泄漏电流

由于实际二极管的材料性质、制造工艺和环境影响等，会在反向电场作用下产生少量的泄漏电流，导致二极管的反向饱和电流比PN结大一些

2.2 温度对特性的影响

当温度升高时，由于本征激发变多，粒子活性高，可以理解为电阻减小，使得正向导通时同等条件下电流变大，二极管正向特性向左移
少子影响明显，导致反向特性向下移

2.3 主要参数

$I_{F}$最大整流电流：二极管长期工作时能通过的正向平均电流的最大值
$U_{R}$最高反向工作电压：二极管最大能够承受的反向电压
$I_{R}$反向电流：未击穿时的反向电流
$f_{M}$最高工作频率：当通过二极管电流频率比这个值高时，由于二极管电容效应的存在，电流通过电容流动，二极管丧失单向导电性

3 二极管的等效电路

3.1 等效电路

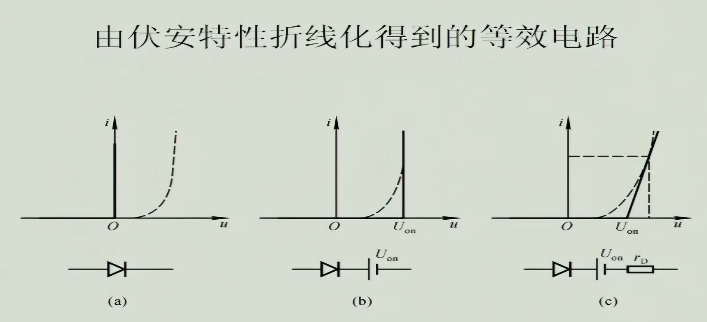
(a)：认为二极管是严格的正向导通方向截止
(b)：由于二极管存在死区，所以给二极管加一个正向的导通电压，舍弃了二极管的压降
(c)：加上了二极管的压降

3.2 正向等效的例子

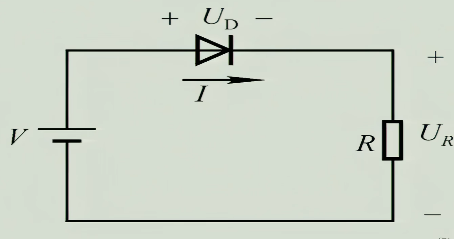
上面这个电路，如果认为这个二极管为理想二极管，则通过二极管的电流为：
$$I=\frac{V}{R}$$
如果使用第二种等效模型且$V$比开通电压$U_{ON}$大，则通过二极管的电流为：
$$I=\frac{V-U_{ON}}{R}$$

3.3 二极管的微变等效

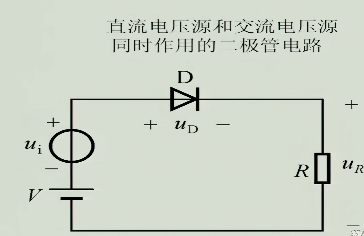
此时如果$u_{i}$的峰值$<U_{ON}$，且只有交流电压源工作，则这个交流电压源根本无法使二极管开通，所以就需要一个直流电压源把交流电压源抬起来，使交流电压工作在能使二极管导通的工作点

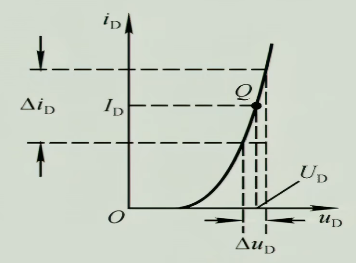
若我们要计算此时输出的电流，若在直流中，我们通常使用欧姆定律$I=\frac{U}{R}$来计算电流，但此时显然直流时电阻无法很明白的表征出来(斜率电阻一直在变化)，但此时若只看交流工作，在一小段$\Delta_{U}$变化范围内，曲线可以近似看为直线，则此时切线斜率就可以近似看做$\frac{\Delta_{U_{D}}}{\Delta_{i_{D}}}=r_{d}$，就可以计算$i_{d}=\frac{U_{i}}{r_{d}+R}$，即在此时，二极管可以等效为一个电阻$r_{d}$，并且$$\frac{1}{r_{d}}=\frac{\Delta_{i_{D}}}{\Delta_{u_{D}}}=\frac{d_{i_{D}}}{d_{u_{D}}}=I_{s} \cdot \frac{1}{U_{T}}\cdot e^{\frac{u_{D}}{U_{T}}}\approx \frac{I_{D}}{U_{T}}$$即$$r_{d}=\frac{U_{T}}{I_{D}}$$我们称电阻$r_{d}$为动态电阻，它的大小与它的静态工作点在哪以及温度相关
于是我们得到了二极管的微变等效的分析方法

3.3.1 微变等效的分析方法

分析直流：只让直流电压源作用分析此时电路所处的静态工作点，使用$I_{D}=\frac{V-U_{ON}}{R}$计算出$I_{D}$
计算动态电阻$r_{d}$：根据静态工作点，计算此时的动态电阻$r_{d}$
分析交流：只让交流电压源作用，此时把二极管用电阻$r_{d}$替代
为了防止迷糊，这里列出几个电流值的意义：
- $I_{D}$：仅直流电压源工作下的电流
- $i_{d}$：仅交流电压源工作下的电流
- $i_{D}$：交直流一起工作下的总电流
  这种分析方法的思想类似于线性网络中的叠加定理，这种思想将在后面也有不少的使用
  
  4 稳压二极管

4.1 特点

可以工作在反向击穿状态下，封装于普通二极管不同，其散热效果较好

4.2 伏安特性

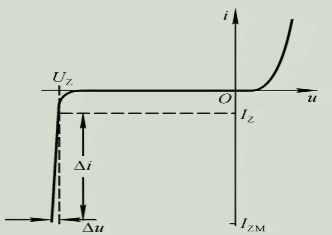
稳压二极管的伏安特性与普通二极管没有什么区别，只不过在反向击穿的时候稳压二极管可以自如的工作

4.3 主要参数

温度系数$\alpha$：$U_{Z}$受温度影响的程度
稳定电压$U_{Z}$：稳压二极管能稳定的电压
最小稳定电流$I_{Z}$：稳压二极管进入反向击穿区的最小反向电流

4.4 稳压二极管的使用

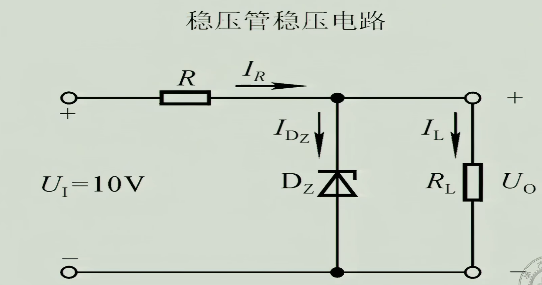
4.4.1 例子

若$U_{Z}=6V$，$R=200\Omega$，$R_{L}=800\Omega$，求$I_{DZ}$
朴素的想，$6V$的稳压二极管，则$U_{DZ}=6V$，$\therefore U_{R}=10V-6V=4V$,$\therefore I_{R}=\frac{U_{R}}{R}=20mA,I_{R_{L}}=\frac{U_{DZ}}{R_{L}}=7.5mA$，$\therefore I_{DZ}=I_{R}-I_{R_{L}}=12.5mA$

但实际上我们得先考虑稳压二极管是否工作在反向击穿状态，若未反向击穿，这么直接计算会出现致命问题，我们应该先设稳压二极管不击穿，计算稳压二极管是否击穿再进行计算

[!WARNING]
稳压二极管不能直接稳压，其稳压作用要借助一个电阻来实现

前情提要（绪论）