本系列笔记仅为个人备忘记录,若要获得最大学习效果仍建议学习郑益慧老师课程:
郑益慧老师课程
如有谬误、补充,还望不吝指正
前面已经讲解了运算放大器的基本的分析原则,接下来其实是用这种分析原则去解决问题
1 基本运算电路
1.1 概述
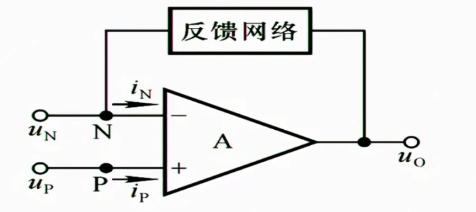
虚短:在深度负反馈情况下,认为$u_{P}=u_{N}$
虚断:一直存在的情况,认为$i_{I}=i_{N}=i_{P}=0$
我们在分析这部分的电路的时候,由于信号源较多,所以经常使用叠加定理来分析
1.2 比例运算
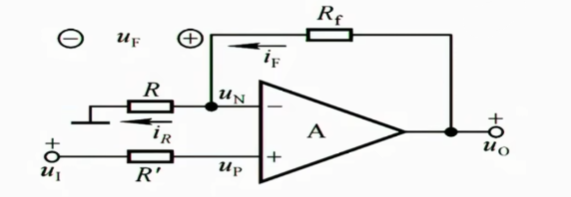
1.2.1 反相比例
1.2.1.1 基本电路
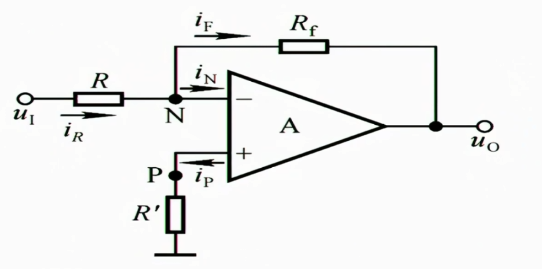
这是个电压并联负反馈,我们要建立$u_{o}$和$u_{i}$之间的关系
首先,由于虚断,$u_{P}=0$
对于$u_{n}$,使用叠加定理:当$u_{o}$置零,$u_{I}$单独作用时
$$
u_{N}=\frac{R_{f}}{R+R_{f}}u_{I}
$$
$u_{I}$置零,$u_{o}$单独作用时
$$
u_{N}=\frac{R_{f}}{R+R_{f}}u_{o}
$$
所以他们两个叠加之后
$$
u_{N}=\frac{R_{f}}{R+R_{f}}u_{I}+\frac{R_{f}}{R+R_{f}}u_{o}=0=u_{P}
$$
$$\therefore u_{o}=-\frac{R_{f}}{R}\cdot u_{I}$$
即这个电路实现了反相比例,一个类似$y=-kx$这种关系的运算
我们如果更加深度的理解虚短虚断的话,可以这样分析:
因为虚短,所以$u_{P}=u_{N}=0$
又因为虚断,因为电位为0,所以电路在N点实际上形成了一个虚拟的地,此时:
$$
i_{R}=\frac{u_{i}-u_{N}}{R}=\frac{u_{i}}{R}
$$即此时输入电压和输入电流成比例,又因为虚断,所以
$$
i_{F}=i_{R}
$$进而因为$\frac{u_{N}-u_{o}}{R_{f}}=i_{f}$
$$
u_{o}=-R_{f}\cdot i_{F}=-\frac{R_{f}}{R}\cdot u_{I}
$$
我们可以从这个分析过程理解这个电路的设计思路,即这个比例关系是怎么传递的
$$
u_{i}\stackrel{R}{\longrightarrow}i_{R}\leftrightarrow i_{f}\stackrel{R_{f}}{\longleftarrow}u_{o}
$$
即$u_{o}$和$u_{i}$通过这个路径形成了一个比例关系
1.2.1.1.1 输入电阻
电阻$R$实际上是在反馈环之外的,如果我站在$R$的后面去等效后面的电路,此时电位为0,电流为$i_{F}$,所以等效电阻为0,和并联负反馈电路的特点相吻合,如果我看这整个电阻的输入电阻,则为反馈电路的电阻加上R,所以$R_{i}=R=\frac{u_{i}}{i_{R}}$
1.2.1.1.2 一个问题
虽然我需要前端是个电流源,但是现在它还是给了个$u_{i}$,这意味着我需要去跟电压源去抢信号,需要输入阻抗足够大,那我们就得提高$R$的大小,但提高$R$的大小会导致要提高$R_{f}$的大小,但是过大的电阻会导致很微小的电流就会导致我的电压有很大的变化,不稳定
如果我想要一个相对大的输入阻抗,但还想保留较高的放大倍数,并且$R_{f}$不能太大,该如何做呢,我让$i_{R}$比$i_{F}$大,于是设计出来如下电路
1.2.1.2 T型网反相比例放大电路
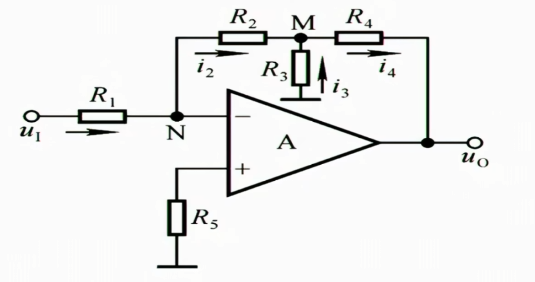
加一个$R_{3}$,提供一个电流来分担压力
要想知道$u_{o}$,我需要知道$i_{4}$和$u_{M}$,$i_{4}$由$i_{2}$和$i_{3}$提供,想要知道$i_{3}$,我需要知道$u_{M}$,如何知道$u_{M}$呢?知道$i_{2}$就可以算出M处电位,所以我只要知道$i_{2}$就能知道一切,$i_{2}=i_{1}$,$i_{1}$和$u_{1}$又存在关系,于是就建立了$u_{o}$和$u_{I}$的关系
1.2.2 同相比例
如果给我们个运放,信号从同相输入端输入,我们需要思考反馈从哪输入,显然如果在同相输入端输入,这个反馈将会是正反馈,所以我的反馈信号必然接在反相输入端上
由于虚短,$u_{P}=u_{i}=u_{N}$
$$
\begin{align}
&i_{R}=\frac{u_{i}}{R}=i_{F} \\
\therefore &u_{o}=u_{N}+i_{F}\cdot R_{f}=(1+\frac{R_{f}}{R})\cdot u_{i}
\end{align}
$$
即我们实现了一个类似$y=kx$的同相比例运算
它是个电压串联负反馈电路,它的输入电阻是无穷,非常适合去取电压信号,但是相比反相比例放大来说,反相比例放大$u_{P}=u_{N}=0$,但这个电路$u_{P}=u_{N}=u_{I}$,即出现了共模信号,需要运放具有比较好的共模抑制能力
为什么会存在一个电阻$R’$,在静态下,实际上同相输入端和反相输入端上面会有一个偏执电流,在反相输入端上,电阻为$R\verb|//|R_{f}$,这意味着$u_{N}$上面会有一个电压,如果没有$R’$,即使同相输入端上有电流,它仍然还是接地的,电位为0,它会导致纯静态下差分输入不为0,可能会对后面电路的运算造成不利影响,为了消除这种影响,我们就在同相输入端上加一个电阻$R’=R\verb|//|R_{f}$,来使两端的电压相等,我们称这个电阻为平衡电阻
1.2.3 电压跟随器
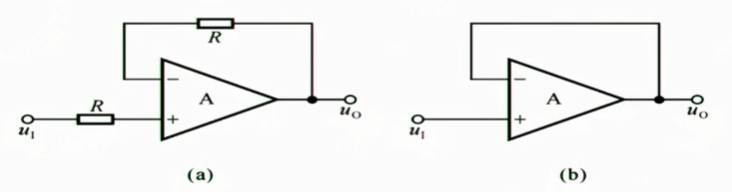
这两个电路求$u_{o}$和$u_{i}$的关系
一眼看过去对于(a)电路,由于虚断,所以上面这个反馈回路上没电流,即$u_{o}=u_{N}$,下面同相输入端也没电流,即$u_{i}=u_{P}$,又因为虚短,$u_{P}=u_{N}$,所以$u_{o}=u_{i}$
1.3 加减
1.3.1 求和电路
1.3.1.1 反相求和
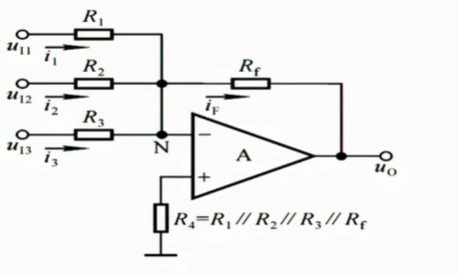
它的设计思想:$u_{11}$,$u_{12}$,$u_{13}$通过$R_{1,2,3}$三个电阻转换为电流信号,这三个电流$i_{1,2,3}$再通过KCL这个求和关系,加和成$i_{F}$,$i_{F}$再通过$R_{F}$转换为$u_{o}$,这就实现了三个电压量的求和
$$
u_{o}=-\left( \frac{R_{f}}{R_{1}}U_{I_{1}}+\frac{R_{f}}{R_{2}}U_{I_{2}}+\frac{R_{f}}{R_{3}}U_{I_{3}} \right)
$$
相当于我们实现了一个$y=-(k_{1}x_{1}+k_{2}x_{2}+k_{3}x_{3})$的运算,这就是反相比例求和电路
1.3.1.2 同相求和
同相求和无非是把输入放到同相输入端,思想是一致的
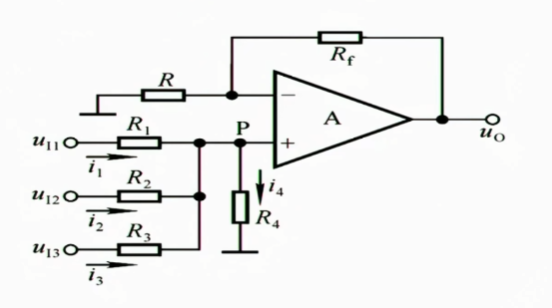
这三路电流决定了$i_{4}$,$i_{4}$决定了$u_{P}$,$u_{P}=u_{N}=u_{o}$,我们可以用叠加定理去分别计算1,2,3的比例关系
1.3.2 加减运算电路
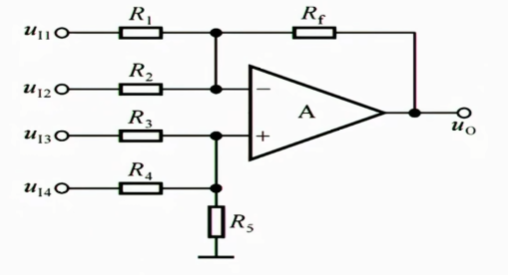
同相端和反相端相互叠加,就是加减运算电路,它的计算也是使用叠加原理分别计算再叠加
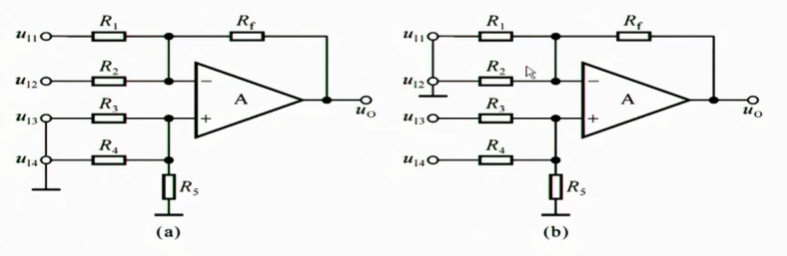
考虑一个定性的问题,即对于$u_{o}$,这四个电压同相输入端上的是加,反相输入端上的是减
1.3.3 差分比例运算电路
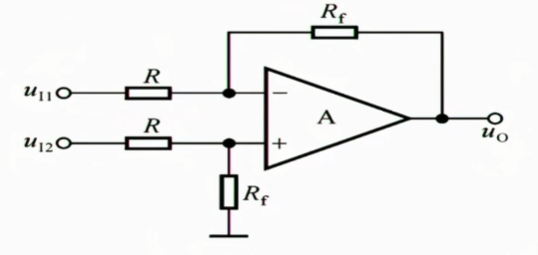
把加减运算电路的加减数量都剩一个,则形成了差分比例放大电路,但是这个电路就造成了一个问题,即同相输入端的输入电阻被破坏了,在这种情况下其输入电阻为$R+R_{f}$,但如果没有这个$R_{f}$,输入电阻反而会变得很大,如果我们希望两端的输入电阻都很大,我们该怎么做呢?
最简单的解决方案就是在前端用两个电压跟随器,这样输入电阻就变大了,以及下面这个解决方案
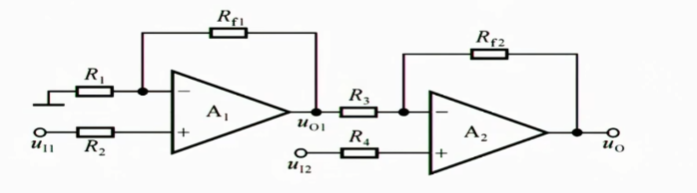
我们使用两路运算放大器,前面是一个同相比例电路,使得$u_{11}$输入电阻变大,$u_{12}$则直接输入,就形成了高输入电阻的差分比例运算电路
1.4 微积分
我们只需要找一种元件,它的电压电流关系满足某种微积分的关系,我再把输出电压和输入电压与它的电流或者电压以比例形式关联,就可以实现一个微积分电路,我们找的这个元件是电容
1.4.1 积分运算电路
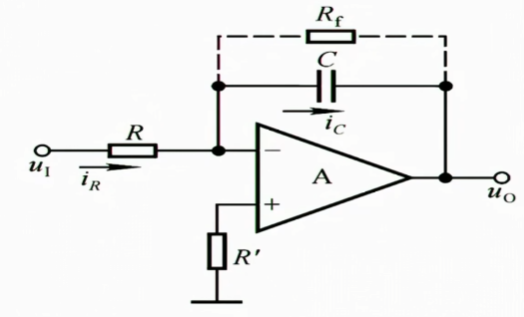
$u_{i}$和$i_{R}$即$i_{C}$成比例,对电容充电,提供$u_{o}$电压,于是此时$u_{o}$就应该等于$\frac{u_{i}}{R}$的一个积分,为什么加$R_{f}$,它在保护电路,使得C不会轻易饱和充电
于是我们就获得了一个能计算积分的电路
1.4.2 微分运算电路
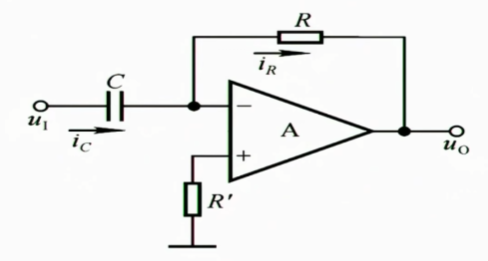
这个电路有不好玩的问题,如果$u_{i}$是一个阶跃的信号的话,则在阶跃的那一瞬间,$i_{C}$趋向于无穷,会让$R$上出现一个巨大巨大的压降,一瞬间就把运放干饱和晕掉了
为了解决这个问题,我们必须改进这个电路,给他加一个保护机制
1.4.2.1 实用微分运算电路
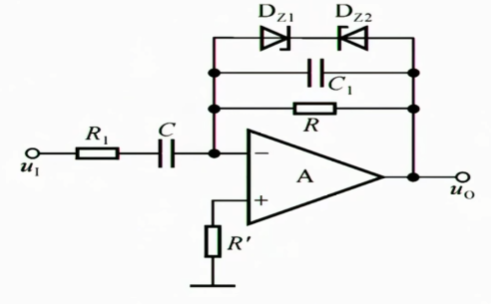
使用稳压二极管来保证$R$的电位不会变得特别特别高,$C_{1}$则用于相位补偿,防止进入自激振荡
1.5 对数、指数
如果有一个元件,其伏安特性是对数或者指数,就可以做出对数、指数运算电路,这个元件是二极管,或者用三极管取代
1.5.1 对数运算电路
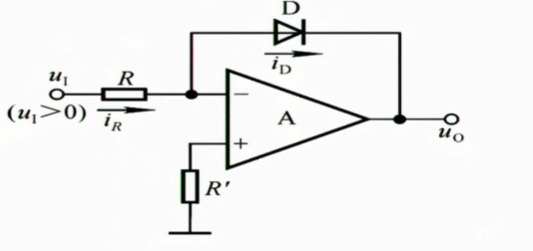
二极管的电压范围有限,很多时候我们使用三极管来代替二极管
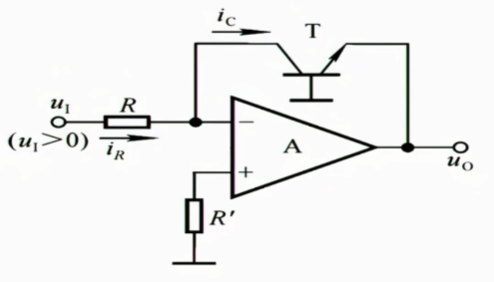
1.5.2 指数运算电路
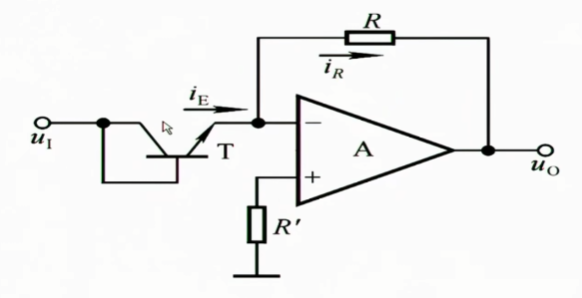
1.6 逆函数型微分运算电路
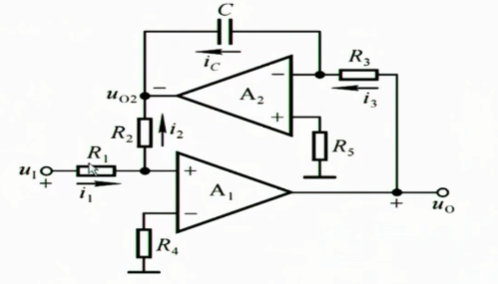
使用反馈把输出和输入掉个个,就可以完成反函数的效果
2 运算电路设计思路
设计思路:
- 找到一种元器件,通过这个元件电压和电流的关系作为核心来构建电路,我们先后找到了三种元件,代表比例的电阻,代表微积分的电容,代表指数对数的二极管,根据这些关系,我们利用虚短虚断的概念就可以构建一个运算电路,加减则使用KCL的原理去加减
- 通过反馈把输入和输出对换,实现逆函数的效果来构建运算电路
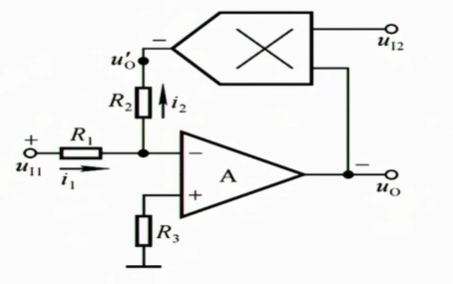
3 模拟乘法器

假设我们要计算$u_{I_{1}}\cdot u_{I_{2}}$,我们可以如下这样算:
$$
\begin{align}
&\ln{u_{I_{1}}}+\ln{u_{I_{2}}}=\ln{u_{I_{1}}\cdot u_{I_{2}}} \\
&e^{\ln{u_{I_{1}}\cdot u_{I_{2}}}}=u_{I_{1}}\cdot u_{I_{2}}
\end{align}
$$
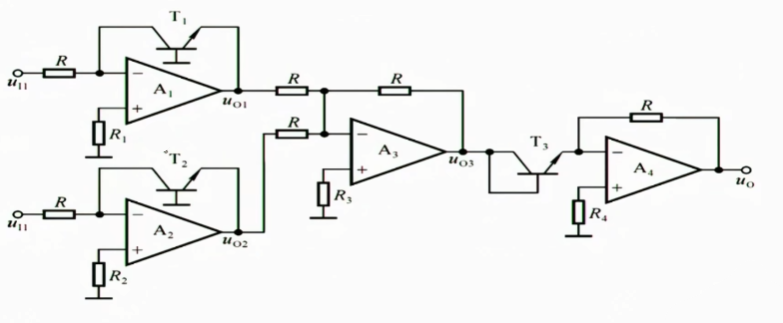
3.1 简介
3.1.1 电路及符号
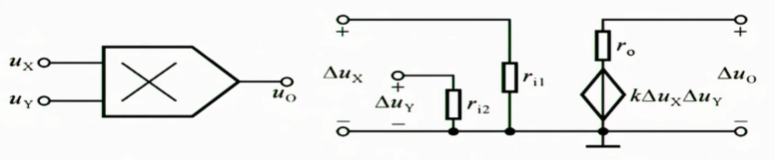
3.1.2 理想
输入电阻无穷大,输出电阻极小,k值趋向稳定
$$
\Delta u_{o}=k\Delta u_{x}\cdot\Delta u_{y}
$$
3.1.3 不理想
模拟乘法器对输入是有约束的
3.2 应用
3.2.1 乘方运算
3.2.1.1 平方运算
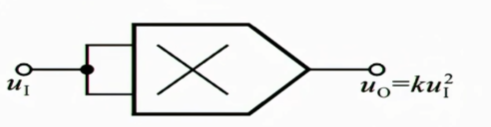
3.2.1.2 三次、四次方运算

3.2.1.3 N次方
使用指数和对数

3.2.2 除法
使用逆函数的设计思维,基于乘法电路构造除法电路