本文最后更新于 432 天前,如有失效或谬误请评论区留言。
本系列笔记仅为个人备忘记录,若要获得最大学习效果仍建议学习郑益慧老师课程:
郑益慧老师课程
如有谬误、补充,还望不吝指正
前部分的几节大量说了半导体器件的构成和特性,但实际上应试的重点从本节开始
基本放大电路的构成
1 放大的概念
1.1 特征
放大的特征一定是功率的放大而不是仅仅电压或仅仅电流的放大变化
1.2 本质
把小功率信号(小电压、小电流)变成大功率信号(大电压,大电流)
能量在控制下的一种转换,是对能量的控制和转换
1.3 必要条件
需要一个外部电源(能量)
需要一个用于控制能量的元件$\to$有源元件,如三极管、场效应管等,并且要处于正确的工作状态
需要一个合理的输出,使得放大的信号可以合理的输出出去
1.4 前提条件
对于放大电路来说,最基本的要求是不失真
2 基本共射放大电路
2.1 结构原理
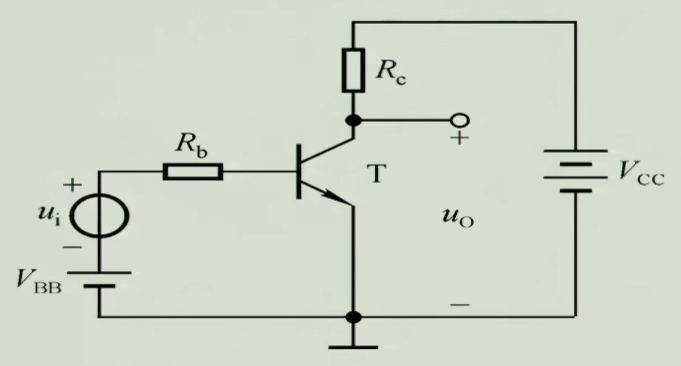
- $V_{BB}$:提供一个直流的偏置,使发射结正偏导通
- $u_{i}$:输入的小信号,由于$V_{BB}$的作用,它可以使输入电流$i_{B}$随自己变化
- $R_{b}$:限流电阻
- $V_{CC}$:使集电结反偏截止,保证三极管工作在放大状态下,提供了放大所需的能量
- $R_{c}$:通过$R_{c}$,把放大后的电流信号转化为电压信号
2.2 直接耦合/阻容耦合共射放大电路
由于基本共射放大电路中存在两个电源,实际使用中一个放大电路两个电压不同的电源很不方便,所以设计了直接耦合共射放大电路,如下图
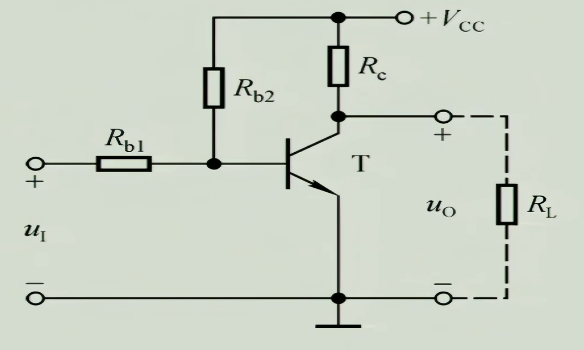
- $R_{b_{1}}$:使得交流信号$u_{1}$可以与直流信号共同作用
- $R_{b_{2}},R_{c}$:通过这两个电阻的分压,使得基极的点位比集电极点位低,保证集电结反偏
- $+V_{CC}$:整个电路的电源
- $R_{L}$:负载
直接耦合指信号直接传递,不通过其他别的东西,导致在输入时效率不高,输出时的电流是直流与交流混杂,并非纯交流
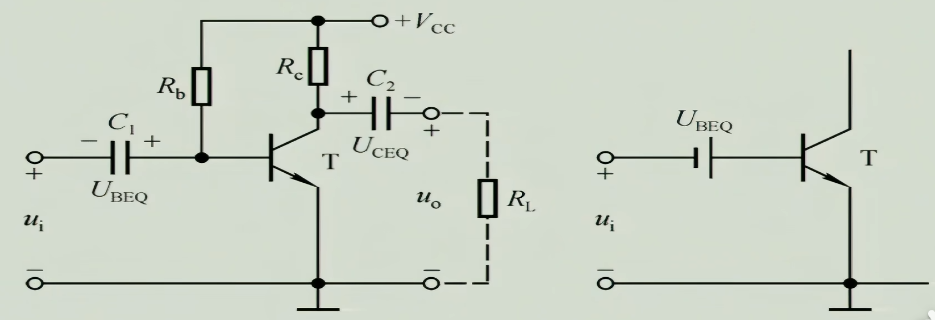
若要获得纯交流的输出,我们可以使用电容来实现,于是我们就得到了阻容耦合共射放大电路
- $C_{1}$:通交隔直,使得直流电流不从左边流走,而是在右边使得集电结正偏导通,并且可以把交流信号叠加上去
- $C_{2}$:通交隔直,实际上形成了一个高通滤波器,使得输出的直流部分被滤除,剩下纯交流部分
放大电路的原理和性能指标
1 放大电路的原理
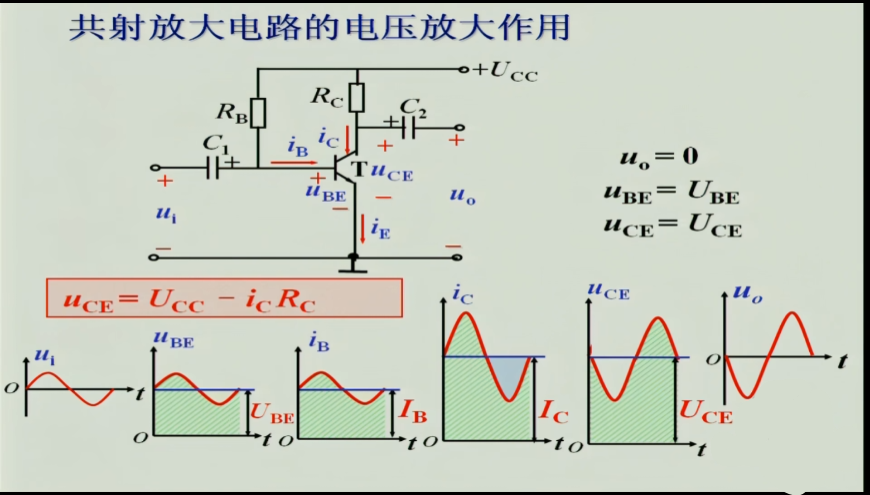
以阻容耦合共射放大电路为例,讲解放大电路的工作原理
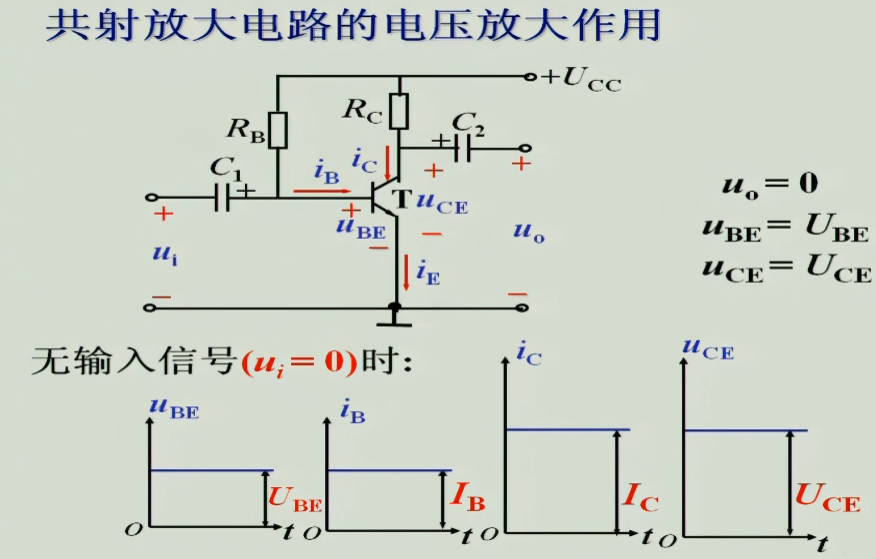
- 先让小交流信号$u_{i}$为0:三极管工作在了放大状态下,此时$C_{1},C_{2}$相当于断路,此时会有一个直流的$u_{BE}$,根据输入特性曲线,一定会有一个对应的直流的$i_{B}$,则对应一个$i_{C}$,对应一个$u_{CE}$
- 给出输入信号:$u_{i}$的变化使得$u_{BE}$变化,进而根据输入特性曲线使得$i_{B}$变化,使得$i_{C}$变化,由于$R_{C}$的分压作用,进而使得$u_{CE}$变化,成功获得放大后的输出
2 放大电路的性能指标
2.1 等效示意图
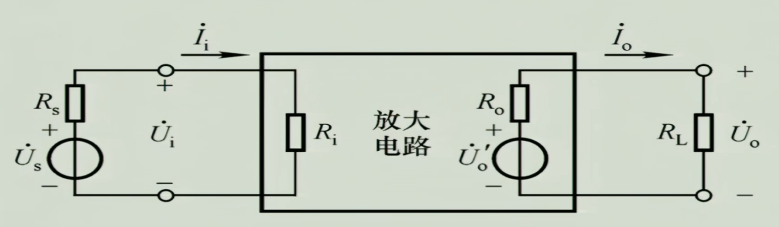
由戴维南定理,放大电路可以等效为上面的等效示意图
- 对于前端电路:可以被等效为一个电压源输入和一个内阻串联/一个电流源输入和一个内阻并联的形式,后面的放大电路则可以被等效看做一个电阻
$$\dot{U_{i}}=\frac{R_{i}}{R_{i}+R_{S}}\dot{U_{S}}$$
由上式,若为一个电压型的输入,$R_{i}$越大,输入的电压$\dot{U_{i}}$越大,并且为了防止输入畸变等问题,需要减少$\dot{U_{S}}$的输出功率,就要减小其输出电流,故对于前端电路来说,输入阻抗越大越好 - 对于负载:前端的所有东西,可以等效为一个电压源和一个内阻输出电阻$R_{o}$串联的形式,当然也可以等效为电流源
2.2 指标
2.2.1 放大倍数
- $\dot{A}_{uu}$:电压放大为电压的放大倍数
- $\dot{A}_{ui}$:电压放大为电流的放大倍数
- $\dot{A}_{iu}$:电流放大为电压的放大倍数
- $\dot{A}_{ii}$:电流放大为电流的放大倍数
2.2.2 电阻
- $R_{i}$:输入电阻
- $R_{o}$:输出电阻
输入输出电阻在多级放大电路相连的时候更为重要,此时,后极的输入电阻为前一级的负载
2.2.3 频率指标
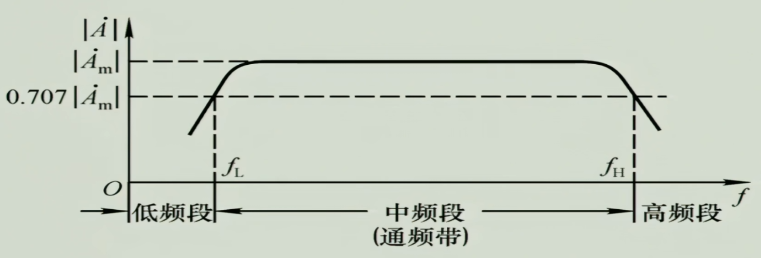
对于阻容耦合而言,若频率越低,则电容会把交流信号也一起削弱,并且对三极管来说,频率太高会由于结电容的存在,导致放大倍数降低,于是就出现了上图中的通频带的曲线
2.2.4 非线性失真
非线性失真这里先不讲
2.2.5 最大不失真输出电压
输出电压再大的话,放大电路就要开始失真了
2.2.6 最大输出功率与效率
电压处于最大不输出电压的时候电路输出的功率和效率
放大电路的分析方法
回忆二极管的微变等效,我们使用了先分析静态工作点在分析该点上的动态工作情况的方式,在这里我们也使用这种思想,有些类似叠加定理(但是并不是叠加定理,因为叠加定理只用于线性电路,这里是非线性电路)
1 直流通路-交流通路
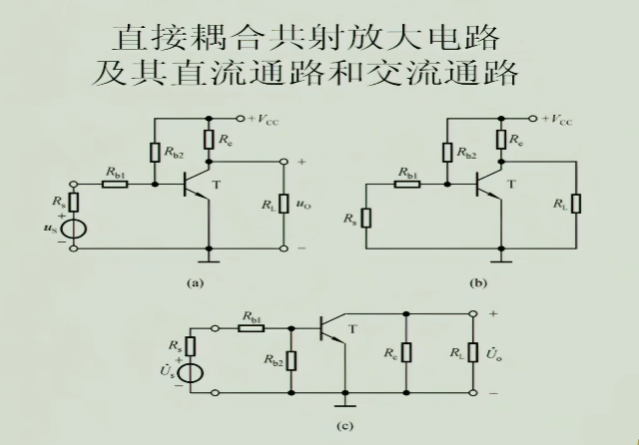
1.1 直流通路
放大电路中直流所流经的通路,把电路中交流信号$u_{i}$置零,此时认为电容为断路,就可以获得直流通路
直流通路可以有效的用于判断电路的静态合不合理,便于分析电路的工作情况,
1.2 交流通路
交流信号所流经的通路,把电路中直流电源置零,此时认为电容为短路,就可以获得交流通路
2 图解法
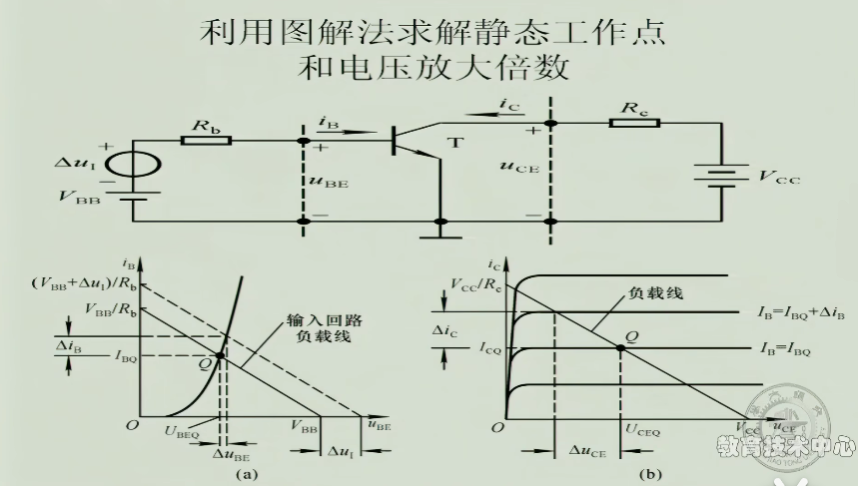
输入要符合两个曲线:
- 三极管的输入特性曲线
- 外部电路界定的方程
输出要符合两个曲线: - 三极管的输出特性曲线
- 外部电路界定的方程
分析过程: - 分析输入回路的静态工作,此时外部回路的方程为$i_{B}=\frac{V_{BB}-U_{BE}}{R_{b}}$,这个曲线会和三极管的输入特性曲线有一个交点,这个交点就是此时三极管的静态工作点,静态电流为$I_{BQ}$
- 于是就可以分析输入回路上的动态过程,可以获得此时的$i_{B}$的变化
- 分析输出回路的工作,此时外部回路的方程为$i_{c}=\frac{V_{CC}-u_{CE}}{R_{c}}$,这个曲线会与输出特性曲线中对应$I_{B}=I_{BQ}$的那一条,交于一点Q,此时Q为输出的静态工作点
- 再把变化的$\Delta_{I_{B}}$拿过来,在静态点上分析,就可以得到输出的$\Delta_{I_{C}}$
我们当然不能一直用图解法,我们需要把三极管等效为一个线性元件来方便我们进行分析
3 等效电路法
3.1 微变等效电路
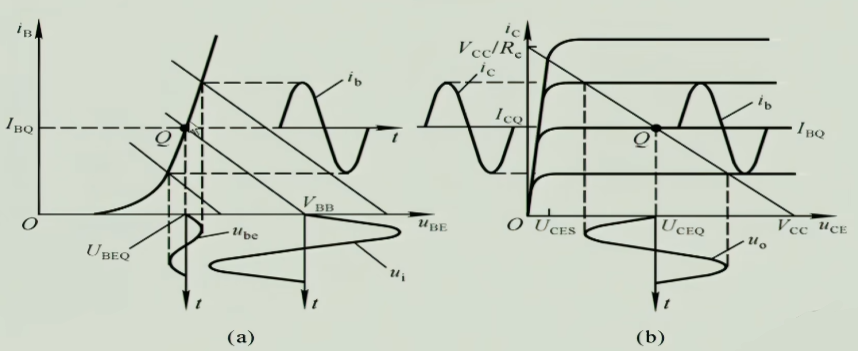
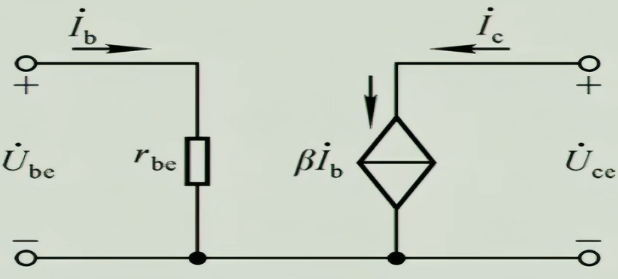
与二极管的微变等效时的动态电阻相同,在分析交流通路时,输入回路的特性曲线在静态工作点Q上的工作状况,我们也可以把他等效成为一个电阻$r_{be}=\frac{\Delta_{u_{BE}}}{\Delta_{i_{B}}}$,用这个电阻$r_{be}$取代发射结来等效,而输出则等效为一个值为$\beta \Delta_{i_{B}}$的受控电流源,下面为具体的分析流程
3.1.1 直流通路
- 得到静态工作点Q点的位置
- 计算出$r_{be}=r_{bb}+\frac{(1+\beta)U_{T}}{I_{EQ}}$,其中$r_{bb}$为基区的体电阻
3.1.2 交流通路
- 作出交流通路
- 把交流通路里的三极管变成一个电阻和一个受控电流源
于是整个电路就可以线性化求解了
3.1.3 几个电流值的区分
- $I_{B}$:直流的静态工作点的输入电流
- $i_{B}$:瞬时值,既有直流又有交流
- $i_{b}$:仅有交流
- $\dot{I_{b}}$:是交流信号的相量
- $I_{b}$:交流信号的有效值
4 H参数等效模型
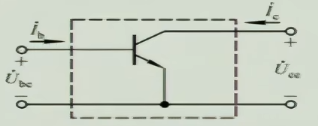
我们需要建立一个数学模型使用数学方法来描述计算动态参数,上图可以认为是一个双口网络,我们可以建立混合参数模型,建立以下方程:
$$
\begin{cases}
u_{BE}=f(i_{B},u_{CE}) \\
i_{c}=f(i_{B},u_{CE})
\end{cases}
$$
即$u_{BE}$与$i_{B},u_{CE}$相关,$i_{c}$与$i_{B},u_{CE}$相关,这个方程是整个特性曲线,但我们想求的是动态的,每个$\Delta$的之间的关系,那么我们对它做全微分
$$
\begin{cases}
\mathrm{d}u_{BE}=\frac{\partial u_{BE}}{\partial i_{B}}\big|_{U_{CE}}\cdot \mathrm{d}i_{B}+\frac{\partial u_{BE}}{\partial u_{CE}}\big|_{I_{B}}\cdot \mathrm{d}u_{CE} \\
\mathrm{d}i_{c}=\frac{\partial i_{c}}{\partial i_{B}}\big|_{U_{CE}}\cdot \mathrm{d}i_{B}+\frac{\partial i_{C}}{\partial u_{CE}}\big|_{I_{B}}\cdot \mathrm{d}u_{CE}
\end{cases}
$$
这玩意谁看了谁迷糊,但如果我们把它都看成$\Delta$呢:
$$
\begin{cases}
\mathrm{d}u_{BE}=\frac{\partial u_{BE}}{\partial i_{B}}\big|_{U_{CE}}\cdot \Delta _{i_{B}}+\frac{\partial u_{BE}}{\partial u_{CE}}\big|_{I_{B}}\cdot \Delta_{u_{CE}} \\
\mathrm{d}i_{c}=\frac{\partial i_{c}}{\partial i_{B}}\big|_{U_{CE}}\cdot \Delta_{i_{B}}+\frac{\partial i_{C}}{\partial u_{CE}}\big|_{I_{B}}\cdot \Delta_{u_{CE}}
\end{cases}
$$
继续改写后
$$
\begin{array}{ll}
\Delta u_{BE}=h_{11}\Delta i_{B}+h_{12}\Delta u_{CE} \\
\Delta i_{c}=h_{21}\Delta i_{B}+h_{22}\Delta u_{CE}
\end{array}
$$
于是就可以重构电路为
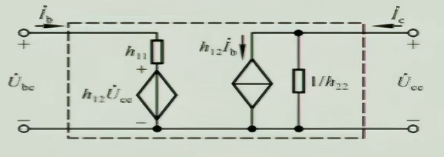
于是我们就获得了H参数等效模型,其中
- $h_{11}=\frac{\partial u_{BE}}{\partial i_{B}}\big|_{U_{CE}}$ :我们知道他是我们前面微变等效时等效出来的$r_{be}$
- $h_{12}=\frac{\partial u_{BE}}{\partial u_{CE}}\big|_{I_{B}}$ :这个值当$u_{CE}>1V$时极小,可以忽略
- $h_{21}=\frac{\partial i_{c}}{\partial i_{B}}\big|_{U_{CE}}$ :这个值我们知道它是放大倍数$\beta$
- $h_{22}=\frac{\partial i_{C}}{\partial u_{CE}}\big|_{I_{B}}$ :这是$i_{C}$随$u_{CE}$增加而略微增加的斜率,若负载电阻不是特别特别大,这个值一般可以忽略,认为它是断路
于是我们得到了简化的H参数模型,实际上就是上节所说的微变等效电路
到现在我们应该非常清楚H参数等效模型了,下面将利用这种模型分析各种电路

强