本系列笔记仅为个人备忘记录,若要获得最大学习效果仍建议学习郑益慧老师课程:
郑益慧老师课程
如有谬误、补充,还望不吝指正
这一章的大前提是集成的,多级的放大电路,目标是输出足够大的功率信号
大概的思想是差分放大电路用于抑制输入的温漂等问题$\to$共射放大电路用于放大电压电流$\to$功率输出
差分放大电路
1 直接耦合放大电路
有很多物理量的变化是缓慢的变化,那么在这种情况下我们不能用阻容式或变压器耦合,并且在集成电路中,不能出现大容值的电解电容,我们也需要使用直接耦合,但是直接耦合的有很多缺点:各级静态工作点相互关联,容易受到干扰,所以我们需要克服它
1.1 零点漂移
直接耦合放大电路当输入置零,输出理应动态为0,是一个稳定的信号,但放大电路输出了动态不为0的信号,这种现象叫做零点漂移,简称零飘
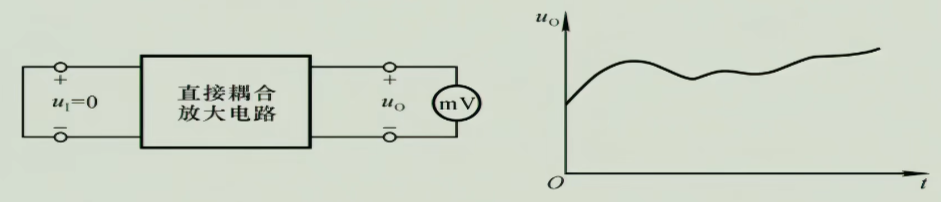
1.1.1 产生原因
温度变化导致静态工作点变化导致零点漂移,称为温飘
1.1.2 抑制温漂的方法
如Q点稳定放大电路,为了抑制温飘,我们引入了负反馈,我们加了个$R_{e}$电阻或者温控的器件,它的好处是确实抑制了温漂,但它对放大效果具有非常大的影响,在直接耦合中我们又不能加一个旁路电容,为了解决这个问题,我们设计了差分放大电路
2 差分放大电路的结构
2.1 设计差分放大电路的过程
既然你动态工作点在变化,那我就外加一个可变的电流源,这个可变电流源跟着零飘一起变化以抵消零漂的影响,我们通过把放大电路再镜像一份来实现这种抵消,并且共用一个用于稳定Q点的电阻$R_{e}$(这部分非常巧妙,强烈建议看看郑老师讲这部分的过程)
2.2 结构
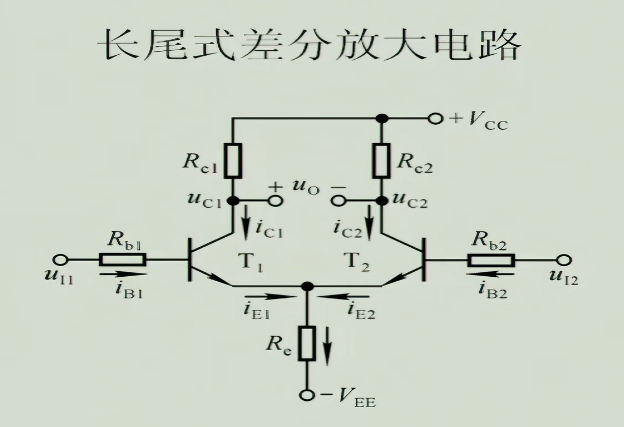
- $u_{o}$:此时的输出电压为左右两边放大电路输出的差,所以使用这种输出方式时,两边输入信号应该反相
- $R_{e}$:可以说是差分放大电路的核心,直流通路下,它可以稳定静态工作点;交流通路下当输入共模信号(一模一样的信号,一般来说是干扰项,如温飘)时,$i_{E1}$和$i_{E2}$共同作用,对于单边放大电路来看的话,相当于$R_{e}$被等效为了两倍,显著降低了此时的放大倍数,把干扰信号有效的消灭掉,当输入差模信号(反相的信号输入)时,$i_{E1}$和$i_{E2}$相互抵消,$R_{e}$上面没有电流,被等效为断路,即不会影响到有用的信号
即如果有干扰的信号输入进来,就可以分成两部分,一部分是共模信号,它被有效抑制,一部分是差模信号,它被有效放大
3 差分放大电路的分析
3.1 共模输入
采用双端输出,$u_{i1}=u_{i2}$时,两边输出相减抵消,$u_{o}=0$,$A_{uc}=0$
3.2 差模输入
$u_{i1}=-u_{i2}$,画它的交流通路,并做H参数等效(这个画交流通路的过程请看视频理解,这里不赘述)
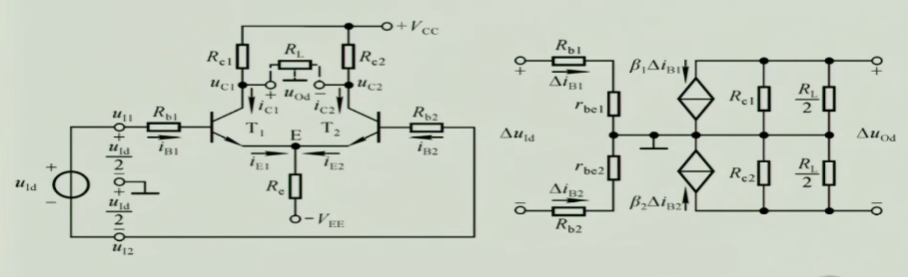
$$A_{ud}=\frac{u_{o}}{u_{id}}=\frac{-2\beta \cdot i_{b_{1}}\cdot R_{c}\verb|//|\frac{R_{L}}{2}}{2i_{b_{1}}\cdot(R_{b}+r_{be_{1}})}$$
它和基本共射放大电路的放大倍数近乎相等,损失非常小
3.3 电压传输特性
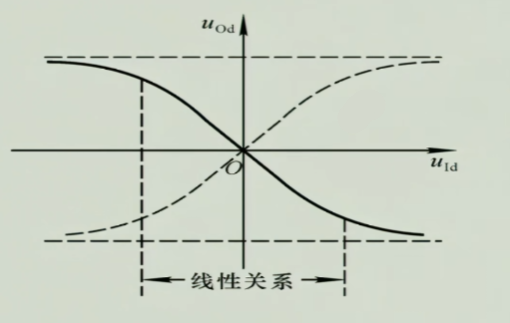
4 其他接法
4.1 双端输入,单端输出
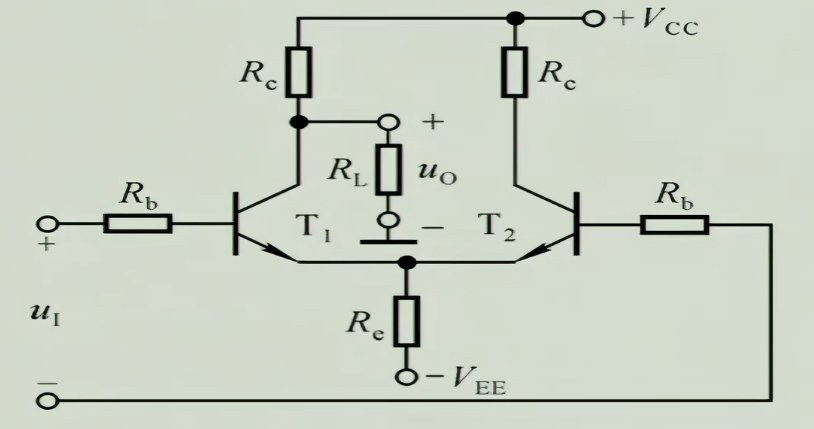
架设给出信号$u_{i}$(既有干扰信号又有正常信号,即既有共模又有差模,分为$u_{IC}+u_{ID}$),要计算$u_{o}$
因为它是单端输出,所以共模信号不会被相减消去,此时只由$R_{e}$来对抗共模信号
此时输出$u_{o}$也被分为两份,一份是差模的$u_{od}$,一份是共模的$u_{oc}$
4.1.1 共模
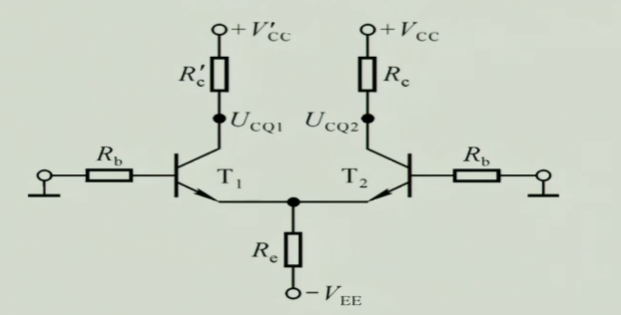
使用直流通路来分析共模部分,因为共模,直流下$R_{e}$等效为两倍,可以把$R_{e}$等效为$2R_{E}$,然后把右边电路抛掉不看,画出交流通路
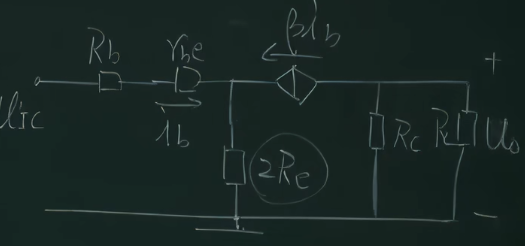
$$A_{oc}=\frac{-\beta R_{c}\verb|//|R_{L}}{R_{b}+r_{be}+(1+\beta )\cdot 2 \cdot R_{e}}$$
所以此时$A_{oc}$非常非常非常小,意味着此时共模被强烈的抑制了,所以其实就算使用单端输出,共模的干扰也非常小
4.1.2 差模
此时差模输出很简单,$R_{e}$被等效掉了,但是此时其输出是普通共射放大电路的$\frac{1}{2}$
4.2 单端输入,双端输出
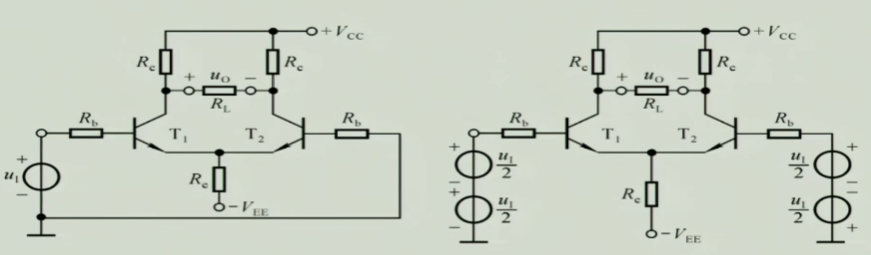
左边输入为$u_{i}$,右边为0,但是我们可以把左边等效分成两个电源$\frac{1}{2}u_{i}$,把右边等效为两个相反的电源一个$-\frac{1}{2}u_{i}$一个$\frac{1}{2}u_{i}$,就可以用双端输入双端输出的分析方法来分析它
4.3 单端输入,单端输出
相当于双端输入单端输出的分析方法如上面一样带一个共模信号
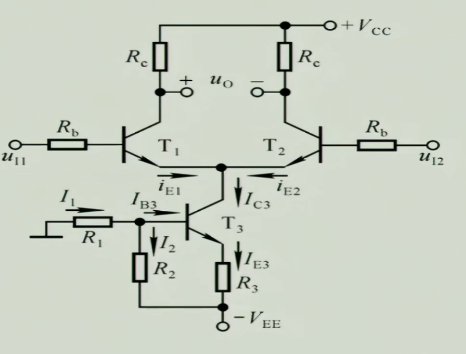
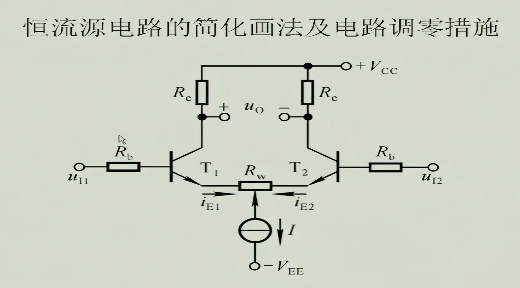
5 具有恒流源的差分放大电路
但是现在出现了一个问题,我们把$R_{e}$不断的加大,但是随着它的增大我们必然要提高$V_{EE}$,如果$V_{EE}$不够大,提供不了足够的直流静态工作点,所以我们需要找一个能提供恒定电流,并且电阻大的电流源,于是我们就设计出了具有恒流源的差分放大电路
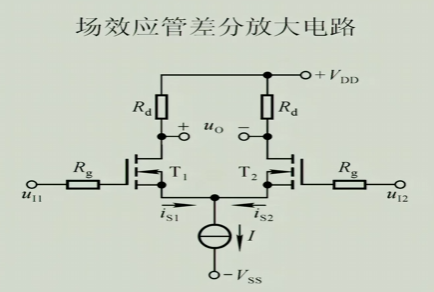
6 场效应管差分放大电路
如果我们想要更大的输入电阻,我们就可以把三极管换成MOS管
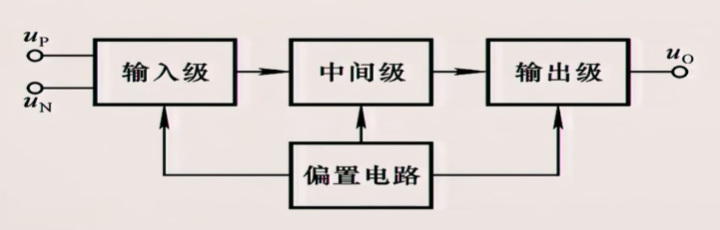
集成运放的概述
集成运放,可以实现模拟型号的比例,加减乘除,微积分,对数等运算的集成元件,它是纯模拟的,还可以进行波形发生、波形整形,有源滤波、整流,非常强大
它是一个集成的,高增益的放大器
1 电压传输特性
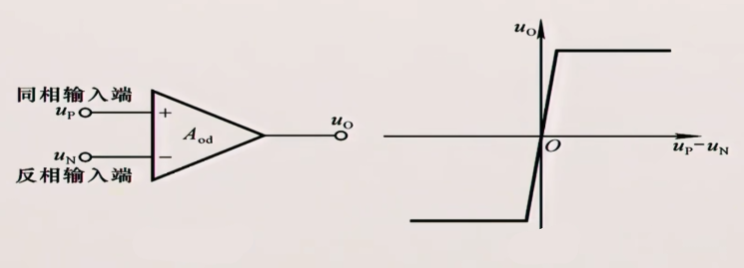
它有一个同相输入端,一个反相输入端,它真正的输入是$u_{P}-u_{N}$,即一个差分信号的输入
它的传输特性中间一段是很窄的线性端,两端饱和
开环放大倍数:$u_{o}=A_{od}\cdot(u_{P}-u_{N})$ 条件是运放工作在线性区
如果只开环的话,这玩意压根没啥用,但是当我们闭环的话,奇迹就出现了,这方面的内容在[[第十节-运算放大器]]
集成运放的电流源电路
我们希望$R_{c}$电阻尽量大使得我电压放大倍数尽量高,但是$R_{c}$电阻如果太大对电源会造成较大的压力,我们需要提高电源电压,所以为了解决这个两难问题,我们使用一个电流源来代替$R_{C}$电阻,我们需要设计这个电流源
1 基本电流源
1.1 镜像电流源
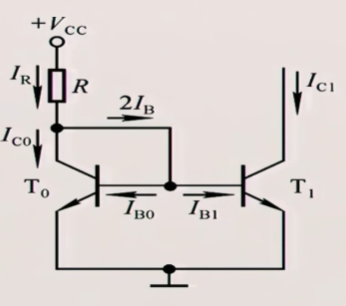
$T_{0}$和$T_{1}$是对管,特性一模一样,$u_{BE_{0}}=u_{BE_{1}}$,所以$I_{B_{0}}=I_{B_{1}}$,所以$I_{C_{0}}=I_{C_{1}}$
$$I_{R}=I_{C}+2I_{B}=I_{C}+\frac{2I_{C}}{\beta}=\frac{\beta+2}{\beta}\cdot I_{C}$$$$I_{R}=\frac{V_{CC}-V_{BE_{0}}}{R}$$
所以我们可以使用$I_{R}$来控制$I_{C_{1}}$的输出
但当我要求$I_{C_{1}}$很大的时候,就需要$I_{R}$一样大,导致$R$上面有一个巨大的电功率,全部用来发热,就导致出现散热问题了,所以我们需要想想如何用小电流控制大电流,于是就出现了比例电流源
1.2 比例电流源
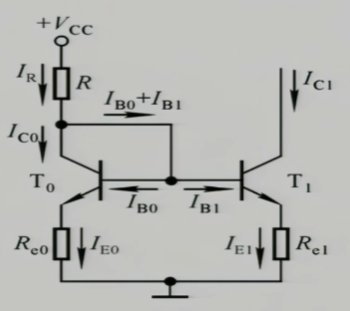
比例电流源与镜像电流源的区别就是多塞了两个电阻上去,对于下面这个回路我们列出一个KVL方程
$$I_{E_{0}}\cdot R_{e_{0}}+U_{BE_{0}}=I_{E_{1}}\cdot R_{e_{1}}+U_{BE_{1}}$$
$U_{BE_{0}}$与$U_{BE_{1}}$这俩都是导通电压,近似相等,所以上式可化简看做
$$I_{E_{0}}\cdot R_{e_{0}}=I_{E_{1}}\cdot R_{e_{1}}$$
即
$$\frac{I_{E_{0}}}{I_{E_{1}}}=\frac{R_{e_{1}}}{R_{e_{0}}}$$
即他们中间有一个比例关系,这个比例关系就直接传递给了$I_{C_{1}}$和$I_{C_{0}}$
$$\frac{I_{C_{0}}}{I_{C_{1}}}=\frac{R_{e_{1}}}{R_{e_{0}}}$$
又$I_{R}=I_{C_{0}}+I_{B_{0}}+I_{B_{1}}$当$\beta$很大时,$I_{B_{0}},I_{B_{1}}$可以忽略,$I_{C_{0}}\approx I_{R}$,所以我们就实现了$I_{R}$对$I_{C_{1}}$的比例控制
$$I_{C_{1}}=\frac{R_{e_{0}}}{R_{e_{1}}}\cdot I_{C_{0}}\approx\frac{R_{e_{0}}}{R_{e_{1}}}\cdot I_{R}$$
所以就实现了用一个小的$I_{R}$控制大的$I_{C}$
我们现在考虑完了大电流,再来考虑小的几十微安的电流源怎么做,比例电流源是反比关系,如果我们想要$I_{C_{0}}$很小,就得让$R_{e_{0}}$变得很小或者$R_{e_{1}}$变得很大,但是如果电阻太大会导致它分压变多,所以我们选择让$R_{e_{0}}$变得很小,即把它短路,于是就构成了微电流源
1.3 微电流源
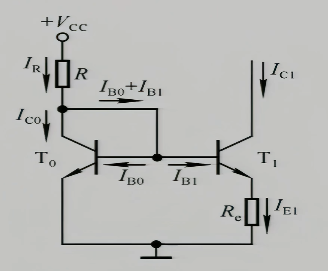
$$U_{BE_{0}}=U_{BE_{1}}+I_{E_{1}}\cdot R_{e}$$
所以
$$I_{E_{1}}=\frac{U_{BE_{0}}-U_{BE_{1}}}{R_{e}}$$由于$U_{BE_{0}},U_{BE_{1}}$十分相近,所以这个分子几乎是0,$I_{E_{1}}$的值将非常非常非常小,但是此时我们得思考怎么用$I_{R}$来控制它的大小
$$\because I_{E}=I_{S}\cdot (e^{\frac{u}{U_{T}}}-1)\approx I_{S}\cdot e^{\frac{u}{U_{T}}}$$
$$\therefore U_{BE_{0}}=U_{T}\cdot \ln{\frac{I_{E_{0}}}{I_{S}}},U_{BE_{1}}=U_{T}\cdot \ln{\frac{I_{E_{1}}}{I_{S}}}$$
$$\therefore U_{BE_{0}}-U_{BE_{1}}=U_{T}\cdot \ln {\frac{I_{E_{0}}}{I_{E_{1}}}}$$
$I_{E_{0}}$出现了,那事情就好办了,当$\beta$很大很大时$I_{C_{0}}\approx I_{E_{0}}$
$$\therefore I_{C_{1}}=\frac{U_{T}}{R_{e_{1}}}\cdot \ln{\frac{I_{R}}{I_{C_{1}}}}$$
我们现在讨论的前提是$\beta \gg 2$,但是现实生活中,受限于工艺技术等因素,我们的管子的$\beta$可能没有那么大,所以我们就要寻求改进电路,使得左边管子分出的那一支通往基极的电流尽量小,但是流入基极的电流大小还要大,那就加个放大电路呗,因为要放大电路,所以加一个射极输出器,于是设计出了加射级输出器的电流源这样的改进型电流源
2 改进型电流源
2.1 加射级输出器的电流源
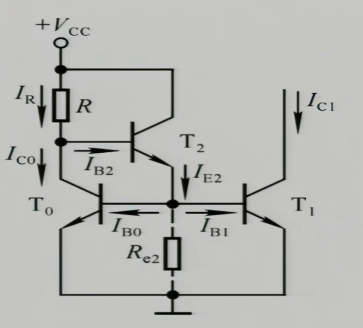
$R_{e_{2}}$的作用是,$I_{B_{0}}$和$I_{B_{1}}$可能非常小,因为$I_{E_{2}}$提供了这两个电流,所以$I_{E_{2}}$也非常小,所以此时T2的放大倍数可能没有到我们预想的那个$\beta_{2}$,就外加一个补偿电阻给他提供一点点电流以获得更高的放大倍数
2.2 威尔逊电流源
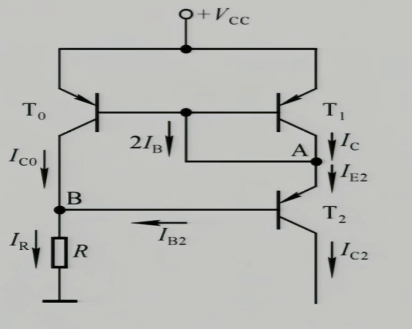
$$I_{E_{2}}=2I_{B}+I_{C}=\frac{\beta+2}{\beta}I_{C}$$
$I_{C_{2}}$是输出,$I_{C_{2}}=\frac{\beta}{\beta+1}I_{E_{2}}$
$$
I_{R}=I_{C_{0}}+I_{B_{2}}=I_{C}+\frac{I_{E_{2}}}{\beta +1}
$$
所以就能推出$I_{R}$和$I_{C_{2}}$的关系:
$$
I_{C_{2}}=I_{R}\left( 1-\frac{2}{\beta^{2}+2\beta+2} \right)
$$
出现了一个高次项$\beta^{2}$,即此时即使$\beta=10$,右边这个系数还是很小,我们几乎可以认为
$$
I_{C_{2}} = I_{R}
$$
即威尔逊电流源解决了$\beta$的问题,但它还不止解决了这一个问题,我们现在要输出的是$I_{C_{2}}$,所以我们一定要让他恒定,稳定
对于T2来说,上面的$I_{E_{2}}$的输入相当于一个大电阻的电流源,充当了我们之前说过的Q点稳定的放大电路的那个$I_{e}$,所以此时$I_{C_{2}}$的温度稳定性非常非常高
3 多路电流源
我们上面说的这些电流源都是一个$I_{R}$控制一个电流源,但在真正的集成电路里面我们会需要很多电流源,所以我们希望一个$I_{R}$可以控制很多电流源,这就出现了多路电流源电路
3.1 基于比例电流源的多路电流源
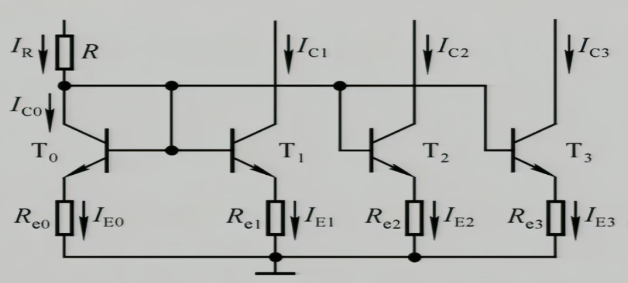
3.2 多级电极管构成的多路电流源
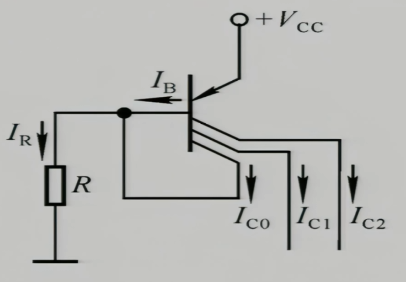
3.3 MOS管多路电流源
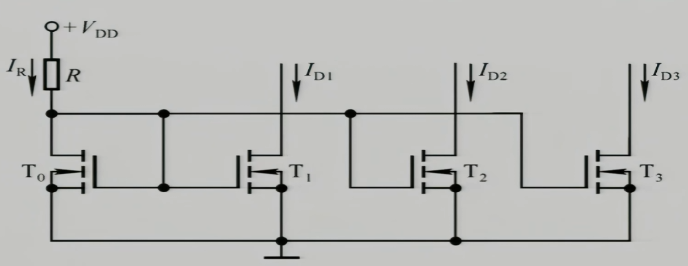
4 以电流源为有源负载
(理想)电流源的特点:
- 输出电流为固定值,这是它的本身属性
- 输出电压为任意值,且输出电压由外部电路和电流源共同决定
- 电流源内阻为无穷
我们使用电流源的时候可以把它看成一个巨大巨大的电阻
4.1 有源负载共射放大电路
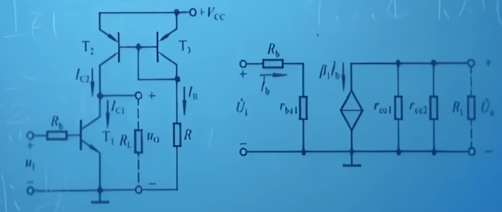
左边图是一个共射放大电路,它和普通的共射放大电路相比,它缺了两个东西:$R_{C}$和$V_{CC}$电源,也就是说缺了我$I_{C}$从哪来的问题,从哪来呢,从电流源来:
上面这个镜像电流源提供了$I_{C}$和$R_{C}$电阻,但是问题就来了,此时$I_{C}$想受两个东西控制:$I_{B}$要控制$I_{C}$,上面镜像电流源$I_{R}$也要控制$I_{C}$,所以两者需要匹配
再来看右边的等效电路,此时等效出来了两个电阻$r_{ce_{1}}$和$r_{ce_{2}}$,它们一个是e和c之间的动态电阻(这个电阻在之前的H参数等效中,因为它过于大,被视为开路,但是此时电流源的内阻也非常大,可以与它媲美,所以在这里显形),一个是电流源的内阻,他们两个电阻很大,所以就会把电路的放大倍数提的很高
4.2 有源负载差分放大电路
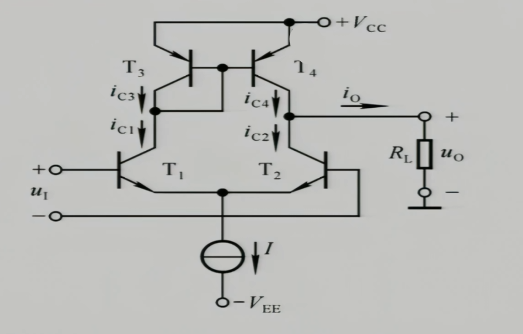
差分信号进去,$i_{C_{1}}$和$i_{C_{2}}$应该是反的,但是上面部分电路是一个镜像电流源,所以(以下公式全是动态情况下,懒得写$\Delta$了)$I_{C_{1}}\approx I_{C_{3}}\approx i_{C_{4}}$
$$
i_{O}=i_{C_{4}}-i_{C_{2}} \because i_{C_{2}}=-i_{C_{1}}=-i_{C_{3}}=-i_{C_{4}} \therefore i_{O}=2i_{C_{4}}
$$
当共模信号出现的时候,最终造成的结果就是$i_{C_{4}}=i_{C_{2}}$,即没有$i_{O}$了
这样的电路就和双端输出有异曲同工之妙
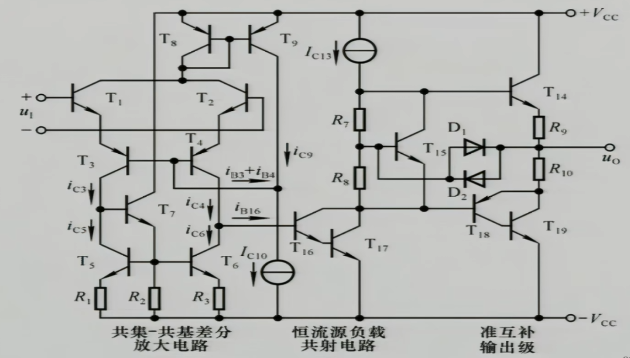
5 挑战:看懂以下电路
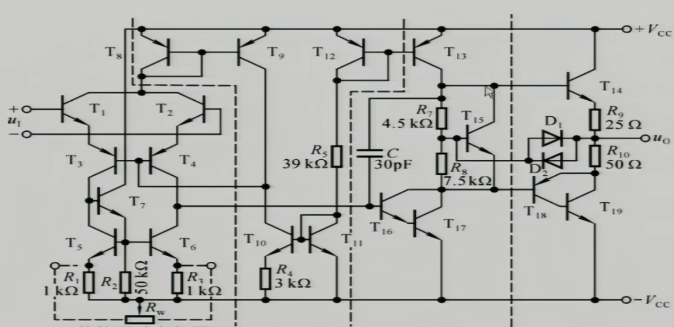
最后一部分是一个互补输出级的功放;往前走,$T_{15}$这里是一个倍增电路用于克服交越,$T_{16},T_{17}$是一个复合管的共射放大电路,其$R_{C}$电阻用上面$T_{9},T_{12}$构成的镜像电流源取代;再往前走一级是两个电流源电路,$R_{5}$控制两个电流源,上面是一个镜像电流源,下面是一个微电流源;再往前走是一个差分放大电路的输入级,上面是提供静态的电流源,中间是共集-共基放大电路,下面是一个比例电流源
评论