本文最后更新于 53 天前，如有失效或谬误请评论区留言。

1 树的基本概念和术语

层次(树型)结构，一对多，它的特点是一个数据元素若有直接前驱，只能有一个直接前驱，一个数据元素若有直接后继，可以有多个直接后继

1.1 树的定义

递归定义：具有以下相同特性的n个结点(数据元素)的有限集合：

若$n=0$，则树是空树，否则
- 存在唯一的称为根的结点root
- $n>1$时，其余结点可分为m个互不相交的有限集$T_{1},T_{2},\dots,T_{m}$，其中每个子集本身又是一颗符合本定义的树，称为根root的子树
- m棵子树的根节点为根root的直接后继

1.2 树的表示法

树的表示法很多，包括二元组、图示、集合、广义表等

二元组表示法如$Tree=(D,S)$，其中

$$
\begin{array}{ll}
D=\left\{ A,B,C,D,E,F,G,H,I,J,K,L,M \right\} \\
S=\left\{ <A,B>,<A,C>,\dots,<J,M> \right\}
\end{array}
$$

即D表示树的结点，S表示树结点之间的连接关系

图示表示法就是直接把树的结构画出来

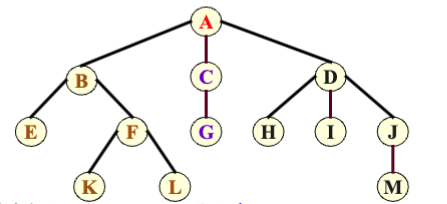
1.3 术语

结点：数据元素+若干指向子树的分支
结点的度：分支的个数，子树的个数
树的度：树中所有结点的度的最大值
叶子结点：度为零的结点
分支结点：度大于零的节点
结点路径：由从根到该结点所经过分支和结点构成
孩子结点，双亲结点，兄弟结点，堂兄弟，祖先结点，子孙结点：字面意思
结点的层次：若根节点的层次为1，往下一层加一层
树的深度：树中叶子结点的最大层次
森林：是m棵不相交的树的集合，一颗非空的树把根节点拔掉，剩下的就是个森林

2 二叉树

二叉树就是一棵树，但是任意一个结点的度最大为2，也就是说每个分支结点最多有两个孩子，可以只有一个或者没有，空树和只有根结点的树也是二叉树

2.1 二叉树的性质

二叉树的第i层上至多有$2^{i-1}$个结点$(i\geq1)$
深度为k的二叉树上至多包含$2^k-1$个结点
任何一颗二叉树，若它含有$n_{0}$个叶子结点、$n_{2}$个度为2的结点，则必存在关系式$n_{0}=n_{2}+1$

2.2 两类特殊二叉树

满二叉树：所有结点除了叶子结点，度都为2，即深度为k，含有$2^k-1$的二叉树
完全二叉树：二叉树从左上到右下渐满，即一个结点的两个孩子必须先有左子树再有右子树，不允许只有右子树
- 有n个结点的完全二叉树的深度为$\lfloor \log_{2}n \rfloor+1$
- 根节点是1，每层从左向右一次排号，则对于任何一个编号为i的结点，$2i$结点是这个结点的左孩子，$2i+1$是右孩子,$\left\lfloor \frac{i}{2} \right\rfloor$的结点是其双亲结点(以上三个的前提是没有溢出，这些东西存在)

2.3 存储结构

2.3.1 顺序存储表示

用一个一维数组存放二叉树的每个结点，每个结点在数组中的位置为高度相同的满二叉树中对应节点的层次编号

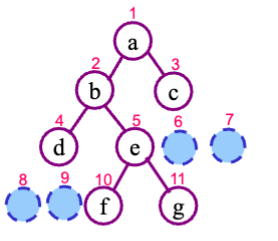
如上述这个树就可以用一个一维数组表示，数组下标就是编号-1，其中5、6、7、8空着

#define MAX_TREE_SIZE 100 // 最大结点数
typedef TElemType SqBiTree[MAX_TREE_SIZE];

但是这种方式存在一个问题，如果是单枝树的花，就会导致数组大小很大但是只有很少的几个空间里有元素。会导致大量的存储浪费

2.3.2 链式存储表示

链表的表示形式很直观，结点内存值和指针，有以下几种

二叉链表：结点内存左子树根和右子树根，这种方法找子孙结点容易，找祖先节点麻烦
三叉链表：结点内存左子树根、右子树根和双亲节点
双亲数组：双亲数组存放二叉树，一个数组元素存放二叉树中一个结点，存放结点的值、其双亲的存放位置（在数组中的下标），以及他是其双亲的左还是右孩子

3 遍历二叉树和线索二叉树

3.1 遍历二叉树

3.1.1 遍历二叉树的方法

遍历二叉树即把二叉树的所有结点都访问一遍，分为四种遍历方法，其中三种我们可以从递归的角度去理解：

先(根)序遍历：对于一棵树，先访问它的根节点，然后对左树执行先序遍历，再对右树执行先序遍历
中(根)序遍历：对于一棵树，先对左树执行中序遍历，再访问它的根节点，然后，再对右树执行中序遍历
后(根)序遍历：对于一棵树，先对左树执行后序遍历，再对右树执行后序遍历，最后访问根节点

这里给出先序遍历的实现方法，其他两个大同小异只是顺序变了而已

void PreOrder(BiTree T){
    if(T){// T非空
        visit(T); // 访问T，这里可以是任何操作
        PreOrder(T->lchild); // 遍历左子树
        PreOrder(T->rchild); // 遍历右子树
    }
}

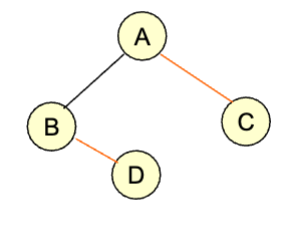
可以对着这棵树试验一下上面的遍历方法，这里给出各个方法的遍历序列：

先序：ABDC
中序：BDAC
后序：DBCA
另外一种遍历方法是层次遍历，即一层一层的从左往右的遍历完所有结点

3.1.2 遍历二叉树的应用

可以用于计算二叉树中叶子节点的个数，遍历过程中计数没有左右孩子的结点即可
求二叉树的高
用二叉树存放表达式，遍历二叉树输出前缀中缀和后缀

3.1.3 相关结论

树中结点都不相同的情况下，先序+中序或者后序+中序·可以唯一确定一颗二叉树

3.1.4 二叉树的建立

可以用先序序列定义一颗二叉树，在先序序列中加入空树的明确表示，例如用’#‘表示，如果只有右子树没有左子树，左子树的位置就用#表示

3.1.5 非递归实现前中后序遍历

递归容易理解，但执行速度较慢，我们可以用非递归的方式实现上面几个遍历，只需要借助栈即可：

先序遍历非递归算法的实现：访问根结点后，在访问左子树前，应保存其非空右子树，把它压入栈中，然后访问左子树，若左子树为空的话，就访问栈顶并出栈
中序遍历非递归算法的实现：在访问根结点的左子树前，应保存根结点，如此左子树访问结束后，可以找到根结点，访问根结点和根的右子树
后序遍历非递归算法的实现：访问根结点的左子树前，应保存其根结点，以便左子树访问结束后，访问根的右子树和根

同样这里给出先序的实现方式，其他两个大同小异

#define MAX 10000
// 栈，用于存放右子树
typedef struct{
    BiTree data[MAX];
    int top
}SeqStack;
void PreorderTraverse(BiTree T){ // T为二叉树的根节点
    SeqStack s;
    s.top=-1;
    // 初始化一个栈
    BiTree p = T; // 从根节点开始遍历
    while(p){
        while(p){
            visit(p); // 访问p结点，这里可以是任何语句调用任何函数
            if(p->rchild){ // p有非空右孩子
                if(s.top == MAX-1)
                    exit(0); // 栈满溢出
                else
                    s.data[++s.top] = p->rchild;
            } 
            p = p->lchild; // 访问左孩子
        }
        if(s.top!=-1)
            p=s.data[s.top--] // 左孩子(当前的p)为空，开始找栈里保存的右孩子
    }
}

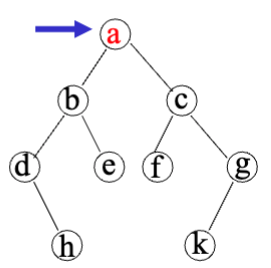
上面是一个例子，它的先序是abdhecfgk，中序是dhbeafckg，后序是hdebfkgca

3.2 线索二叉树

利用二叉链表里的空指针域，存放指向结点在某种遍历次序下的前驱和后继结点的指针(这种指针称为线索)的二叉树叫做线索二叉树，这种二叉链表称为线索链表

根据线索性质的不同，线索二叉树分为先序线索二叉树、中序线索二叉树、后序线索二叉树

线索二叉树的作用是方便遍历操作，确定了遍历的第一个节点，后续操作只需要查找当前节点在遍历序列中的直接后继，反之最后一个结点后序操作就是查找当前节点的直接前驱

这种结构的问题在于结点里的指针非空我们不知道它表示的究竟是他的孩子还是其后继，这个时候我们可以添加两个变量LTag和RTag，用于指示lc和rc里存储的是线索还是孩子指针

typedef enum {Link,Thread} PointerTag;
// Link == 0 ->指针 ; Thread == 1 -> 线索
typedef struct BiThrNod{
    TElemType data;
    struct BiThrNode *lc,*rc; // 左右指针
    PointerTag LTag,RTag; // 左右标志
} BiTheNode, *BiThrTree

将二叉树变为线索二叉树的过程称为线索化，按某种次序把二叉树线索化的实质是按该次序遍历二叉树，在遍历过程中用线索取代空指针

4 树和森林

4.1 树的存储结构

4.1.1 双亲表示法

用一维数组存放树中的每个结点的值和双亲位置，结点存放无顺序要求

typedef struct PTNode{
    ElemType data;
    int parent; // 双亲的位置下标
} PTNode;
typedef struct{
    PTNode nodes[MAX_TREE_SIZE];
    int r,n; // r是根节点位置 ， n是结点个数
}PTree;

这种存储方式特点是找祖先容易，找子孙难

4.1.2 数电孩子表示法

存放树中每个结点的值、直接后继的地址

4.1.2.1 定长结点的多重链表

链表存放树中的每个节点的值和孩子结点的位置(childi，表示这个结点的第i个孩子的指针，表示逻辑关系)

每个结点的孩子指针的个数 = 树中孩子最多的结点的孩子个数 = 树的度，这就导致了整个存储结构可能存在很多空指针，浪费空间，但是整个树的结构统一

4.1.2.2 不定长结点的多重链表

基本思路和上面一样，但是变成了结点有多少个孩子就开多少空间，所有树中每个结点的链表的长度可能不同，结点结构不统一，操作较复杂

4.1.2.3 孩子单链表表示法

将每个结点的所有孩子结点拉成一个单链表，用数组来存储节点们，每个数组元素的data字段存放树种结点的值，firstchild存其孩子单链表的头指针，但是这样会出现结点存了两次的问题，所以为了节省存储空间，方便更新和数据维护，每个数组元素只在数组中存放一次，孩子单链表中不存储指针而是存储这个结点在数组中的下标位置

可以把孩子单链表和双亲表示法结合在一起，给每个数组元素添加一个字段，存放其双亲结点在数组中的位置

4.1.3 二叉链表(孩子-兄弟)表示法

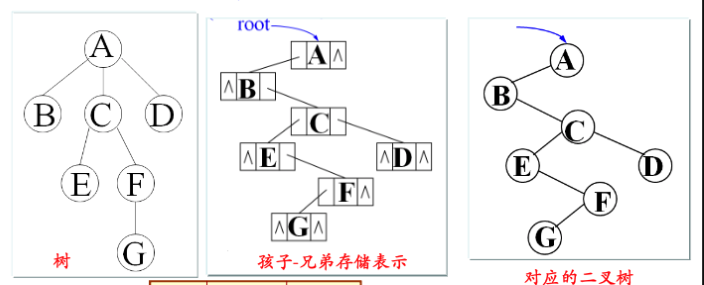
typedef struct CSNode{
    ElemType data; // 数据域
    struct CSNode *fc,*nb; // fc是长子指针域 ， nb是右邻兄弟指针域
}CSNode,*CSTree;

树以孩子兄弟表示法存储，相当于把这个树转换成了二叉树，但这个二叉树根节点没有右子树，这就可以借助二叉树的操作实现树的操作

4.2 森林和二叉树的转换

森林由多棵树组成：$F=(T_{1},T_{2},\dots,T_{n})$，将每棵树用孩子-兄弟表示法，转换成二叉树$BT_{1},BT_{2},\dots,BT_{n}$。没课二叉树的根的右子树都是空树，从$BT_{n}$开始依次将其根节点的前驱链为前一棵二叉树的根的右孩子，最后就会变成一整颗二叉树，然后森林的操作就可以借助二叉树的操作完成

4.3 树和森林的遍历

树的遍历可以有三条路径：

先根(次序)遍历：若树不空，则先访问根节点，然后依次访问它的各个子树
后根(次序)遍历：若树不空，则先依次访问它的各子树，再访问根节点
按层次遍历：一层一层自上而下自左向右遍历每个结点

森林的遍历有两条路径：

先序遍历：若森林不空，先访问森林中第一棵树的根节点，然后对第一棵树的子树构成的森林做森林的先序遍历，然后再先序遍历除了第一棵树之外其余树构成的森林，最后得到的序列和该森林转化为的二叉树的先序序列一样
中序遍历：若森林不空，对第一棵树的子树构成的森林做森林的中序遍历，然后访问第一棵树的根节点，然后再中序遍历除了第一棵树之外其余树构成的森林，最后得到的序列和该森林转化为的二叉树的中序序列一样

5 哈夫曼树

离散学了一遍，数电又学了一遍，懒得写了，看一道之前做过的哈夫曼树的模型题吧

5.1 P1090 NOIP 2004 提高组合并果子

5.2 题目描述

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 $n-1$ 次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 $1$ ，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有 $3$ 种果子，数目依次为 $1$ ， $2$ ， $9$ 。可以先将 $1$ 、 $2$ 堆合并，新堆数目为 $3$ ，耗费体力为 $3$ 。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 $12$ ，耗费体力为 $12$ 。所以多多总共耗费体力 $=3+12=15$ 。可以证明 $15$ 为最小的体力耗费值。

5.3 输入格式

共两行。
第一行是一个整数 $n(1\leq n\leq 10000)$ ，表示果子的种类数。

第二行包含 $n$ 个整数，用空格分隔，第 $i$ 个整数 $a_i(1\leq a_i\leq 20000)$ 是第 $i$ 种果子的数目。

5.4 输出格式

一个整数，也就是最小的体力耗费值。输入数据保证这个值小于 $2^{31}$ 。

5.5 输入输出样例 #1

5.5.1 输入 #1

3 
1 2 9

5.5.2 输出 #1

5.6 说明/提示

对于 $30\%$ 的数据，保证有 $n \le 1000$：

对于 $50\%$ 的数据，保证有 $n \le 5000$；

对于全部的数据，保证有 $n \le 10000$。

5.7 题目分析

这道题是典型的哈夫曼树的模型，贪心的思想，我们需要保证每次合并果子的时候，我们合并的都是最小的那堆和倒数第二小的，这样就可以保证：此次合并消耗体力最少，下次在合并这堆大果子的时候消耗体力小，这就是构建哈夫曼树的操作

5.8 代码实现

#include<bits/stdc++.h>
using namespace std;
int n,m,ans;
priority_queue<int,vector<int>,greater<int> > q; // 优先队列，相当于小根堆，用于每次选出两个最小的果子堆
int main(){
    // 读入数据
    cin >> m; // 堆数
    for (int i = 1;i <= m;i++){
        int t;
        cin >> t;
        q.push(t);
    }
    while(q.size() > 1){
        // 找出最小和次小的两堆(哈夫曼树中就是找出根节点权值最小和次小的两个树)
        int t1 = q.top(); q.pop();
        int t2 = q.top(); q.pop();
        // 合并两堆(哈夫曼中就是合并两个树为一个二叉树)
        ans += t1 + t2;
        q.push(t1 + t2);
    }
    cout << ans << endl;
    return 0;
}