1 数组
1.1 数组的定义
k维数组$D=\{ a_{j_{1},j_{2},\dots,j_{k}} |k>0\}$称为数组的维数,$b_{i}$是数组第i维的长度,$j_{i}$是数组元素第i维的下标,$a_{j_{1},j_{2},\dots,j_{k}}$属于ElemSet
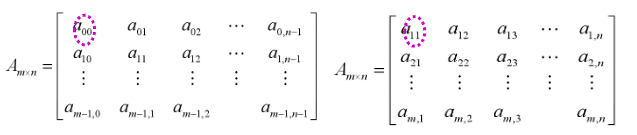
数组可以看做一个特殊的线性表,即线性表数据元素本身又是一个线性表,即数组有多维
数组的结构是固定的,在定义完之后每一维的大小不可变,且数组结构元素同构
数组的运算:
- 给定一组下标,存取,修改其中的数据元素
- 一般不做插入、删除操作
1.2 数组的顺序存储结构
二维数组有两种顺序映像的方式:
- 以行序为主序:从数组的第一行开始顺次存储第一行的数组元素,存储其他行的时候,按照列数顺次存储,这种方法存储的二维数组中任意元素$a_{i,j}$的存储位置是$$Loc(a_{ij})=Loc(a_{11})+[(i-1)n+(j-1)]\times L$$
其中$Loc(a_{11})$称为基地址或者基址
- 以列序为主序:从数组的第一行开始依次存放每一行的数组元素,存放第i行时,从第一列开始顺次存放,这种方法存储的二维数组中任意元素$a_{i,j}$的存储位置是$$Loc(a_{ij})=Loc(a_{11})+[(j-1)m+(i-1)]\times L$$
将二维数组的这两种存储方式推广到一般情况,很好推
由于存在上述的存储方式,所以数组显然支持随机存取,因为通过$Loc(a_{ij})$可以直接算出每个元素的内存地址
#define MAX_ARRAY_DIM 8
typedef struct{
ElemType *base; // 数组元素基地址
int dim; // 数组维数
int *bounds; // 数组维界基地址
int *constants; // 常数C基地址
}Array;
2 矩阵
2.1 矩阵压缩存储
宗旨是为值相同的矩阵元素只分配一个空间,对零元不分配存储空间,最好仍然能够随机存取
2.1.1 特殊矩阵
特殊矩阵中非零元的分布有一定规则
2.1.1.1 上三角矩阵
其特点是$i>j$时$a_{ij}=0或C$
存储方式和二维数组的存储方式类似,分为行为主序和列为主序,分配一个一维的存储空间按照行优先或者列优先的形式依次排列非零元,把二维数组压缩成一维的,然后把下面三角的常数值C保存起来(一般是保存在一维数组的最后一个数组元素)即可
非零元元素的存放地址计算公式如下
$$
Loc(a_{ij})=Loc(a_{11})+\left( \frac{(j-1)j}{2} +i-1\right)\times L
$$
2.1.1.2 下三角矩阵
和上三角矩阵一模一样,只是存放地址公式有变化
$$
Loc(a_{ij})=Loc(a_{11})+\left( \frac{(i-1)i}{2}+j-1 \right)\times L
$$
2.1.1.3 对称矩阵
对称矩阵由于$a_{ij}=a_{ji}$,所以存了上三角阵或者下三角阵相当于存了整个矩阵,所以只需要存上三角阵或者下三角阵就可以了
2.1.1.4 对角矩阵(带状矩阵)
特征:$|i-j| > d$ 时 $a_{ij} = 0$
地址计算公式(下标从1开始):
$$ LOC(a_{ij}) = LOC(a_{11}) + \left[(2d+1)(i-1) + (j-i)\right] \times L $$
2.1.2 稀疏矩阵
矩阵元素的零元多,并且零元在矩阵中随机出现,假设m行n列的矩阵含有t个非零元素,我们可以计算稀疏因子$\delta=\frac{t}{m\times n}$,我们通常认为$\delta\leq0.05$的矩阵为稀疏矩阵
存储稀疏矩阵的原则是:只存储每个非零元的行列下标、值和矩阵的行列维数
2.1.2.1 三元组顺序表
// 三元组结构
typedef struct{
int i,j; // 行列下标
ElemType e; // 值
}Triple;
// 稀疏矩阵顺序表
#define MAXSIZE 100 // 非零元最大个数
typedef struct{
Triple data[MAXSIZE + 1]; // 三元组表
int mu,nu,tu; // 行、列数,非零元数
}TSMatrix;
这个结构就顺应了上面的原则,采取了顺序表+三元组结构来存储有用信息,这个顺序表的要求是,非零元三元组在里面以行为主序顺序存放
如果我们想为这样一个结构的矩阵转置,我们可以采取这种方法:
- 每个三元组的行列下标互换
- 矩阵行列数互换
- 重排顺序表,使得三元组以新的行标从小到大排序
有以下两种实现方法:
- 普通转置:就是每次扫描一遍待转置的矩阵的三元组的列标下的非零元,按序添加到新矩阵里,时间复杂度是$O(nu \times tu)$
-
快速转置(推荐): $O(nu + tu)$
c
Status FastTranspose(TSMatrix M, TSMatrix &T) {
T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
if (!T.tu) return OK;
// 计算列频数 num[col] 和起始位置 cpot[col]
for (col = 1; col <= M.nu; ++col) num[col] = 0;
for (t = 1; t <= M.tu; ++t) ++num[M.data[t].j];
cpot[1] = 1;
for (col = 2; col <= M.nu; ++col)
cpot[col] = cpot[col-1] + num[col-1];
// 转置元素
for (p = 1; p <= M.tu; ++p) {
col = M.data[p].j;
q = cpot[col];
T.data[q] = {M.data[p].j, M.data[p].i, M.data[p].e};
++cpot[col];
}
return OK;
}
2.1.2.2 行逻辑链接顺序表
typedef struct {
Triple data[MAXSIZE];
int rpos[MAXRC]; // 每行首个非零元位置
int mu, nu, tu;
} RLSMatrix;
优势:支持快速访问指定行元素,优化矩阵乘法
2.1.2.3 十字链表
typedef struct OLNode {
int row, col;
ElemType value;
struct OLNode *right, *down; // 同行列后继
} OLNode, *OLink;
typedef struct {
OLink *rhead, *chead; // 行列头指针数组
int mu, nu, tu;
} CrossList;
适用场景:
– 频繁修改矩阵结构(加/减操作)
– 非零元分布动态变化