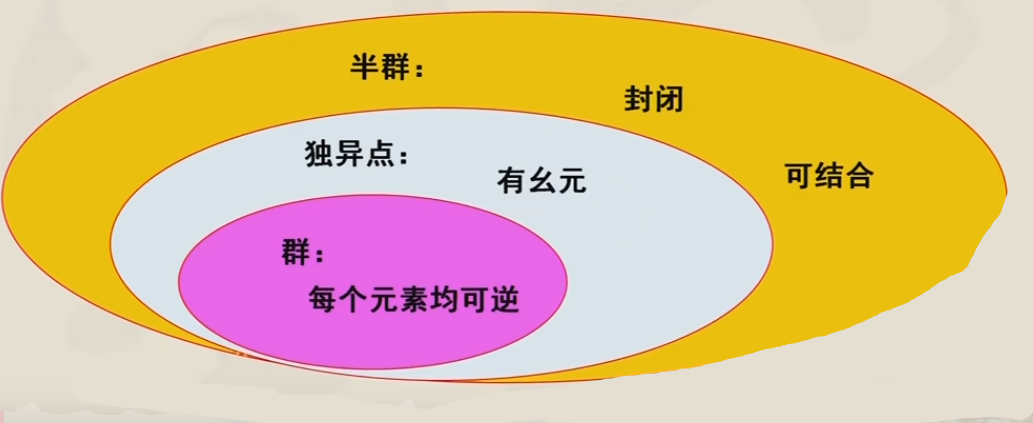
1 半群和独异点

1.1 半群和独异点的定义和性质

1.1.1 半群和独异点

给定代数结构$<S,\odot>$，若运算$⊙$满足结合律，则称$<S,\odot>$为半群

即半群是由集合以及它上面定义的一个可结合的二元运算组成的代数结构

若$<M,\odot>$，若它是半群，且$\odot$有幺元，则称$<M,\odot>$为独异点

所以独异点就是含有幺元的半群，又叫含幺半群，为了强调幺元，独异点可能被表示成$<M,\odot,e>$

1.1.1.1 有限半群

如果半群$<S,\odot>$中的$S$是有限的，则称半群为有限半群

如果一个半群为有限半群，则它存在等幂元，即

$$
<S,\odot >为有限半群 \Rightarrow (\exists x)(x \in S\land x \odot x=x)
$$

1.1.1.2 可交换半群与独异点

给定半群$<S,\odot>$，若$\odot$是可交换的，则$<S,\odot>$是可交换半群

类似的，有可交换独异点$<M,\odot,e>$

1.1.1.3 子半群子独异点

$<S,\star>$是半群，$B\subseteq S$，若$\star$在$B$上封闭，则称$<B,\star>$是$<S,\star>$的子半群，如果幺元$e\in B$，则$<B,\star>$是$<M,\star>$的子独异点

设$<M,\star>$是可交换独异点，$A$是$M$中所有幂等元构成的集合，则$<A,\star>$是$<M,\star>$的子独异点

2 群

2.1 群的定义及其性质

2.1.1 群的定义

$<G,\star>$是代数系统 ，如果$\star$在$G$上满足封闭性，结合性，$<G,\star>$中有幺元且$G$中的每个元素均可逆，则$<G,\star>$是群

• 有限群：$G$是有限集，则对应群是有限群，反之为无限群
• 平凡群：只含有幺元的群
• 若$\star$是可交换的，则$<G,\star>$为可交换群，或阿贝尔群

2.1.2 群的性质

• 群中无零元：因为零元没有逆元，所以群中没有零元
• 群中的每个元素都是可消去元：因为群满足结合性，且每个元素均可逆，所以每个元素都可消去
• 群中除了幺元之外，没有其他幂等元
• 群方程有唯一解：$\exists唯一x \in G$，使得$a\star x=b$，唯一$y \in G$，使$y\star a =b$
• $<G,\star>$是有限群，则$G$中每个元素在$\star$运算表的每一行(列)都必出现且仅出现一次
• $<G,\star>$是个群，对任何$a \in G$，有$(a^{n})^{-1}=(a^{-1})^{n}=a^{-n}$
• $a^{0}=e$

2.1.3 群的阶与群中元素的阶

2.1.3.1 群的阶

设$<G,\star>$是群，如果$|G|=n$，则称它为n阶群

当元素个数是无限的话，它是无限群

2.1.3.2 元素的阶

设$<G,\star>$是群，$a \in G$，使得$a^{k}=e$成立的最小正整数$k$称为$a$的阶，记作$|a|=k$，称$a$为$k$阶元

若不存在这样的$k$，则$a$的阶是无限的

3 子群

3.1 子群及其证明

$<G,\star>$是群，$S$是$G$的非空子集，如何$<S,\star>$满足：

• 封闭性
• 有幺元
• 可逆
  则称$<S,\star>$是$<G,\star>$的子群

3.1.1 平凡子群

任何群$<G,\star>$都存在子群，$<\left\{ e \right\},\star>$和$<G,\star>$都是其子群，称为$<G,\star>$的平凡子群

3.1.2 子群的证明

• 使用定义证明：证明运算在非空子集上满足封闭性，有幺元，子集中元素可逆
• 使用定理证明：
  • $<G,\star>$是群，$B$是$G$的有限子集，如果$\star$在$B$上满足封闭性，则$<B,\star>$是$<G,\star>$的子群
  • $<G,\star>$是群，$S$是$G$的非空子集，如果对任意$a,b\in S$，均有$a\star b^{-1}\in S$，则$<S,\star>$是$<G,\star>$的子群

3.1.3 子群的陪集

$<H,\star>$是$<G,\star>$的子群，$a\in G$，定义集合

$$
\begin{align}
aH=\left\{ a\star h|h\in H \right\} \\
Ha=\left\{ h\star a|h\in H \right\}
\end{align}
$$

则称$aH(Ha)$为$a$确定的$H$在$G$中的左(右陪集)

以下只讨论左陪集，对右陪集有相似的结论

即$0H_{2}=2H_{2}=4H_{2}=\left\{ 0,2,4 \right\}$，$1H_{2}=3H_{2}=5H_{2}=\left\{ 1,3,5 \right\}$，即任意两个左陪集，要么相等，要么不相交

3.1.4 拉格朗日定理

4 循环群

4.1 循环群

$<G,\star>$是群，如果存在一个元素$g\in G$，$\forall x\in G$，都$\exists i,x=g^{i}$，则称$<G,\star>$是循环群，$g$是$G$的生成元

4.2 循环群的类别

• 若$g$的阶是$n$，以$g$为生成元的循环群为$n$阶循环群，称其循环周期为$n$
• 若$g$为无限阶元，则以它为生成元的循环群是无限循环群，并且$<G,\star>$的循环周期是无限的

4.3 循环群生成元的个数

$<G,\star>$是由$g$生成的循环群

• 若$G$是无限循环群，则$G$只有两个生成元$g$和$g^{-1}$
• 若$G$是$n$阶循环群，则$G$含有$\phi(n)$个生成元，且对于任何小于等于$n$且与$n$互素的正整数$r$，$g^{r}$是$G$的生成元($\phi(n)$是欧拉函数，表示小于等于$n$且与$n$互素的正整数的个数)

4.4 循环群的子群

求子群很麻烦，但是求循环群的子群很容易

5 环和域

包含两个代数系统的就是环和域

5.1 环

5.1.1 环的定义

一个代数结构 $<S, +, \cdot >$ 是环的充要条件：

1. $< S, + >$ 是阿贝尔群(交换群)
2. $< S, \cdot >$ 是半群（乘法对合并封闭，具有结合律）
3. $\cdot$对$+$满足分配律：$\forall a, b, c \in S, a \cdot (b + c) = a \cdot b + a \cdot c$

5.1.2 环的性质

零元： 加法群中加法零元，记为0

5.1.3 零因子

在环中，若存在非零元的 $a, b \in S$，使得 $a \cdot b = 0$，则 $a, b$ 为零因子，如果环中所有的$a\cdot b=0$时，$a$或$b$都是零元，则环中无零因子

5.1.4 特殊环

• 若$\cdot$运算满足交换律，则称$<A,+,\cdot>$是交换环
• 若$<A,\cdot>$存在幺元，则称$<A,+,\cdot>$是含幺元
• 若环中无零因子，则称这个环为无零因子环
• 若一个环是交换环，含幺元，无零因子环，则称它是整环
• 如果$<A-\left\{ 0 \right\},\cdot>$是一个交换群，则我们称$<A,+,\cdot>$是域(因为零元没有逆元，如果存在零元，它绝对无法构成群，所以我们要扣掉零元)
  域必是整环，有限整环必是域，无限则不一定

5.2 子环与理想

5.2.1 子环的定义

若 $T \subseteq S$ 且满足：

1. $T$ 对加法封闭（$< T, + >$ 是子群）
2. $T$ 对乘法封闭（$< T, \cdot >$ 是子半群）
   则 $T$ 是 $S$ 的子环。

5.2.2 理想的定义

若 $T$ 是子环且满足：

$$
∀t∈T,∀a∈S,a⋅t,t⋅a∈T∀t∈T,∀a∈S,a⋅t,t⋅a∈T
$$

则 $T$ 称为环 $S$ 的理想

5.2.3 一些特殊性质

• 主理想：存在 $g \in T$，使得 $T = S \cdot g = {a \cdot g \mid a \in S}$
• 交集：若 $T_1, T_2$ 为 $S$ 的理想，则 $T_1 \cap T_2$ 也是 $S$ 的理想
• 商环：对某个理想 $T$，$S/T$ 在适当定义下可以构成一个商环

5.2.4 整数环的主理想

• 主理想说明： 对于整数环 $< Z, +, \cdot >$，其所有理想均为主理想
• 例： 理想 $(n) = {kn \mid k \in Z}$ 的模糊类形式 $a + (n)$ 即为模 $n$ 同余类
• 商环：整数环的商环 $Z/(n)$ 等价于模 $n$ 的环（$< Z_n, +_n, \cdot_n >$）

6 格

7 布尔代数