本文最后更新于 488 天前,如有失效或谬误请评论区留言。
算法复健-第九天
感觉有点过于水了 没什么用 考虑换换刷题顺序 穿插一些洛谷题
Array-Easy-杨辉三角
题面
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
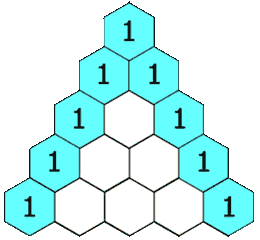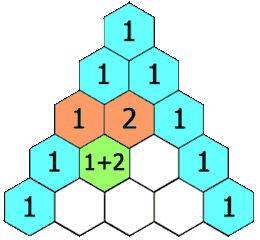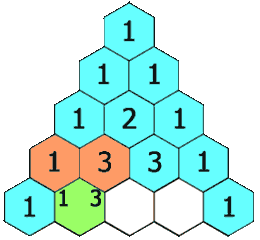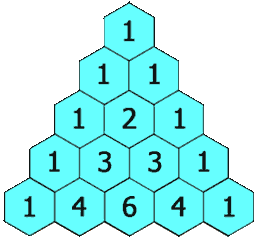
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]示例 2:
输入: numRows = 1
输出: [[1]]提示:
1 <= numRows <= 30
解答过程
本题可以用数学知识解答,用组合数等来推导杨辉三角的公式,但是没必要,通过杨辉三角每个数是左上方和右上方数之和的特性递推解决
代码
vector<vector<int>> generate(int numRows) {
vector<vector<int>> ans(numRows);
for (size_t i = 0; i < numRows; i++)
{
ans[i].resize(i+1 , 1);
for (size_t j = 1; j < i; j++)
{
ans[i][j] = ans[i-1][j-1] + ans[i-1][j];
}
}
return ans;
}Array-Easy-杨辉三角II
题面
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: rowIndex = 3
输出: [1,3,3,1]示例 2:
输入: rowIndex = 0
输出: [1]示例 3:
输入: rowIndex = 1
输出: [1,1]提示:
0 <= rowIndex <= 33
进阶:
你可以优化你的算法到 *O*(*rowIndex*) 空间复杂度吗?
解答过程
本题可以直接推出整个杨辉三角,输出对应行,或者采用推出杨辉三角的递推数学公式,这里使用推出的公式解答
代码
vector<int> getRow(int rowIndex) {
vector<int> ans(rowIndex + 1);
ans[0] = 1;
for (int i = 1; i <= rowIndex; ++i) {
ans[i] = 1LL * ans[i - 1] * (rowIndex - i + 1) / i;
}
return ans;
}Array-Easy-买卖股票的最佳时机
题面
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。提示:
1 <= prices.length <= 10^50 <= prices[i] <= 10^4
解答过程
本题使用贪心的思想,想象如果我们真正买彩票,一定会想我如果能在价格最低的那天买入就好了,所以我们遍历数组,保存目前的最低价格,并且在每天都计算如果卖出可以赚多少钱,取最大值即可
代码
int maxProfit(vector<int>& prices) {
int maxM = 0,minP = 1e9;
for(int price : prices){
maxM = max(maxM,price - minP);
minP = min(minP , price);
}
return maxM;
}