算法复健-第四天

Math-Easy-完美数

题面

对于一个 正整数，如果它和除了它自身以外的所有 正因子 之和相等，我们称它为 「完美数」。

给定一个 整数 n， 如果是完美数，返回 true；否则返回 false。

示例 1：

输入：num = 28
输出：true
解释：28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, 和 14 是 28 的所有正因子。

示例 2：

输入：num = 7
输出：false

提示：

• 1 <= num <= 10^8

解答过程

暴力搜索后发现，本题在10^8的数据范围下只有个位数个解，故暴搜后直接打表

代码

bool checkPerfectNumber(int num) {
        int sum = 0;
        for (size_t i = 1; i < num; i++)
        {
            if (num % i == 0)
            {
                sum = sum + i ;
            }
        }
        if (num == sum)
        {
            cout << num << endl;
            return true;
        }
        return false;
    }

Math-Easy-区间加法II

题面

给你一个 m x n 的矩阵 M 和一个操作数组 op 。矩阵初始化时所有的单元格都为 0 。ops[i] = [ai, bi] 意味着当所有的 0 <= x < ai 和 0 <= y < bi 时， M[x][y] 应该加 1。

在 执行完所有操作后 ，计算并返回 矩阵中最大整数的个数 。

示例 1:

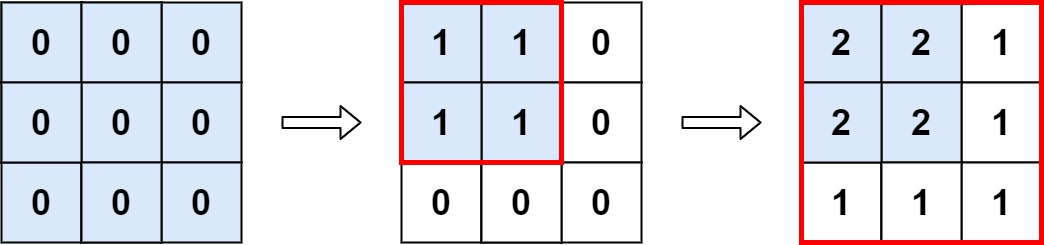
输入: m = 3, n = 3，ops = [[2,2],[3,3]]
输出: 4
解释: M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。

示例 2:

输入: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
输出: 4

示例 3:

输入: m = 3, n = 3, ops = []
输出: 9

提示:

• 1 <= m, n <= 4 * 10^4
• 0 <= ops.length <= 10^4
• ops[i].length == 2
• 1 <= ai <= m
• 1 <= bi <= n

解答过程

读题发现本题加法的区域必包括(0,0)，也就是说这个区域一定是左上角的一个矩形 ， 所以，我们要找最大的整数值的个数，只需要找出最小的矩形，然后再计算出矩形里有多少个数即可

代码

int maxCount(int m, int n, vector<vector<int>>& ops) {
        int mina = m , minb = n;
        for (size_t i = 0; i < ops.size(); i++)
        {
            mina = min(mina , ops[i][0]);
            minb = min(minb , ops[i][1]);
        }
        return mina * minb;
    }

Math-Easy-三个数的最大乘积

题面

给你一个整型数组 nums ，在数组中找出由三个数组成的最大乘积，并输出这个乘积。

示例 1：

输入：nums = [1,2,3]
输出：6

示例 2：

输入：nums = [1,2,3,4]
输出：24

示例 3：

输入：nums = [-1,-2,-3]
输出：-6

提示：

• 3 <= nums.length <= 10^4
• -1000 <= nums[i] <= 1000

解答过程

思考后发现，本题最大的乘数组合要么是三个最大的正数相乘，要么是两个绝对值最大的负数相乘后再乘最大的正数，所以直接遍历一遍数组找出最大的三个数和最小的两个数，再将两种组合的结果取大值即可

代码

int maximumProduct(vector<int>& nums) {
        int MAX1 = -1001 , MAX2 = -1001 , MAX3 = -1001 , MIN1 = 1001 , MIN2 = 1001;
        for (size_t i = 0; i < nums.size(); i++)
        {
            if (nums[i] < MIN1)
            {
                MIN2 = MIN1;
                MIN1 = nums[i];
            }
            else if (nums[i] < MIN2)
            {
                MIN2 = nums[i];
            }

            if (nums[i] > MAX1)
            {
                MAX3 = MAX2;
                MAX2 = MAX1;
                MAX1 = nums[i];
            }
            else if (nums[i] > MAX2)
            {
                MAX3 = MAX2;
                MAX2 = nums[i];
            }
            else if (nums[i] > MAX3)
            {
                MAX3 = nums[i];
            }   
        }
        return max(MIN1 * MIN2 * MAX1 , MAX1 * MAX2 * MAX3); 
    }