算法复健-第三天

Math-Easy-丢失的数字

题面

给定一个包含 [0, n] 中 n 个数的数组 nums ，找出 [0, n] 这个范围内没有出现在数组中的那个数

示例 1：

输入：nums = [3,0,1]
输出：2
解释：n = 3，因为有 3 个数字，所以所有的数字都在范围 [0,3] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 2：

输入：nums = [0,1]
输出：2
解释：n = 2，因为有 2 个数字，所以所有的数字都在范围 [0,2] 内。2 是丢失的数字，因为它没有出现在 nums 中。

示例 3：

输入：nums = [9,6,4,2,3,5,7,0,1]
输出：8
解释：n = 9，因为有 9 个数字，所以所有的数字都在范围 [0,9] 内。8 是丢失的数字，因为它没有出现在 nums 中。

示例 4：

输入：nums = [0]
输出：1
解释：n = 1，因为有 1 个数字，所以所有的数字都在范围 [0,1] 内。1 是丢失的数字，因为它没有出现在 nums中。

提示：

• n == nums.length
• 1 <= n <= 10^4
• 0 <= nums[i] <= n
• nums 中的所有数字都 独一无二

解答过程

本题第一眼可以打个暴力，即先对数组排序后再遍历整个数组，若某个数与其下标不相等，则得出结果，但是显然这个效率极低

为了改进上面的思路，我们可以选择使用哈希表，利用哈希表查找时间复杂度为常数的特性优化代码，总体思路和上面差不多，若最终没有找到重复的数字，则答案为n

发现时间还是有点长，想到可以使用位运算，众所不周知，按位异或是个非常神奇的东西（下面会补充按位异或的性质），我们可以在原数组后面加一个[0,n]的数组，然后对整个数组按位异或，最终得到的结果就是答案

代码

int missingNumber(vector<int>& nums) {
        // 使用哈希表的方法
        unordered_set<int> set ;
        int n = nums.size();
        for (size_t i = 0; i < n; i++)
        {
            set.insert(nums[i]);
        }
        for (size_t i = 0; i <= n; i++)
        {
            if (!set.count(i))
            {
                return i;
            }
        }
        return -1;
        // 使用位运算的方法
        return -1; 
        int res = 0 , n = nums.size();
        for (size_t i = 0; i < n; i++)
        {
            res ^= nums[i];
        }
        for (size_t i = 0; i <= n; i++)
        {
            res ^= i;
        }
        return res;
    }

补充：按位异或的妙用

首先，异或的逻辑是相同则为0，不同则为1，根据他的逻辑，我们可以总结出以下三个特点：

• 0 ^ 0 = 0 , 0 ^ 1 = 1, 0异或任何数=任何数。
• 1 ^ 0 = 1 , 1 ^ 1 = 0 , 1异或任何数=任何数取反。
• 任何数异或自己 = 把自己置0。

根据这三条性质，我们可以这样使用异或：

• 使二进制数某些特定的位数翻转，例如想要把101011001的第二位和第三位翻转 ，就可以把它和000000110做按位异或运算
• 实现两个值的交换而不必使用临时变量(注意此处两个变量若不是整数类型，可能会出现未定义的问题，因为此时交换的是内存地址，并且这样写可读性差，建议只作为学习异或特性的方法来使用)，例如a=a^b,b=b^a,a=a^b就完成了a和b的交换
• 如同本题的，如果将一串数连续异或，由异或运算的可交换性不难得出，出现次数为偶数次的数将消失，最终结果为出现次数为奇数次的所有数的异或

Math-Easy-有效的完全平方数

题面

给你一个正整数 num 。如果 num 是一个完全平方数，则返回 true ，否则返回 false 。

完全平方数 是一个可以写成某个整数的平方的整数。换句话说，它可以写成某个整数和自身的乘积。

不能使用任何内置的库函数，如 sqrt 。

示例 1：

输入：num = 16
输出：true
解释：返回 true ，因为 4 * 4 = 16 且 4 是一个整数。

示例 2：

输入：num = 14
输出：false
解释：返回 false ，因为 3.742 * 3.742 = 14 但 3.742 不是一个整数。

提示：

• 1 <= num <= 2^31 - 1

解答过程

本题当然可以暴力搜索，优化则使用二分搜索优化，没什么好说的

也可以使用数学方法（牛顿迭代法等）解决

代码

bool isPerfectSquare(int num) {
        long l = 1 , r = num ;
        while (l <= r)
        {
            int mid = (l + r) / 2;
            long long sq = (long)mid * mid;
            if (sq > num)
            {
                r = mid - 1;
            }
            else if (sq < num)
            {
                l = mid + 1;
            }
            else
            {
                return true;
            }

        }
        return false;
    }

Math-Easy-排列硬币

题面

你总共有 n 枚硬币，并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯，其第 i 行必须正好有 i 枚硬币。阶梯的最后一行 可能 是不完整的。

给你一个数字 n ，计算并返回可形成 完整阶梯行 的总行数。

示例 1：

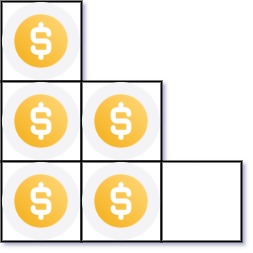
输入：n = 5
输出：2
解释：因为第三行不完整，所以返回 2 。

示例 2：

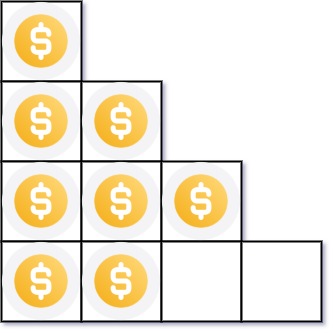
输入：n = 8
输出：3
解释：因为第四行不完整，所以返回 3 。

提示：

• 1 <= n <= 2^31 - 1

解答过程

本题当然当然也可以直接打一个暴力，优化也还是还是二分

本题也可以用数学方法解答，等差数列公式即可，小学数学题

代码

int arrangeCoins(int n) {
        int left = 1, right = n;
        while (left < right) {
            int mid = (right - left + 1) / 2 + left;
            if ((long long) mid * (mid + 1) <= (long long) 2 * n) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        return left;   
    }